AB is a line segment and line l is its perpendicular bisector. If a point P lies on l, show that P is equidistant from A and B.
To show that point P is equidistant from points A and B when P lies on the perpendicular bisector l of line segment AB, we can follow these steps:
1. Identify the Given Information:
- Let A and B be the endpoints of the line segment AB.
- Let C be the midpoint of segment AB.
- Line l is the perpendicular bisector of segment AB.
2. Understand the Properties of the Perpendicular Bisector:
- Since l is the perpendicular bisector of AB, it means that:
- AC=BC (the lengths from A to C and from B to C are equal).
- The angle ∠ACB is 90∘ (the line l is perpendicular to AB).
3. Consider the Triangles:
- We will consider triangles APC and BPC.
- We need to show that PA=PB.
4. Identify the Common Side:
- The segment PC is common to both triangles APC and BPC.
5. Establish the Congruence of the Triangles:
- We have:
- AC=BC (as C is the midpoint).
- ∠PCA=∠PCB=90∘ (since l is the perpendicular bisector).
- PC=PC (common side).
- Therefore, by the SAS (Side-Angle-Side) congruence criterion, triangles APC and BPC are congruent.
6. Conclude the Result:
- Since triangles APC and BPC are congruent, their corresponding parts are equal.
- Thus, PA=PB.
Final Conclusion:
Since PA=PB, we have shown that point P is equidistant from points A and B.
---
- Let A and B be the endpoints of the line segment AB.
- Let C be the midpoint of segment AB.
- Line l is the perpendicular bisector of segment AB.
- Since l is the perpendicular bisector of AB, it means that:
- AC=BC (the lengths from A to C and from B to C are equal).
- The angle ∠ACB is 90∘ (the line l is perpendicular to AB).
- We will consider triangles APC and BPC.
- We need to show that PA=PB.
- The segment PC is common to both triangles APC and BPC.
- We have:
- AC=BC (as C is the midpoint).
- ∠PCA=∠PCB=90∘ (since l is the perpendicular bisector).
- PC=PC (common side).
- Therefore, by the SAS (Side-Angle-Side) congruence criterion, triangles APC and BPC are congruent.
- Since triangles APC and BPC are congruent, their corresponding parts are equal.
- Thus, PA=PB.
Since PA=PB, we have shown that point P is equidistant from points A and B.
Topper's Solved these Questions
Similar Questions
AB is a line segment and line l is its perpendicular bisector. If a point P lies on l, show that P is equidistant from A and B.
View SolutionAB is a line segment and line l is its perpendicular bisector. If a point P lies on l, show that P is equidistant from A and B.
View SolutionA line segment is symmetrical about its perpendicular bisector.True or false?
View SolutionTo construct the perpendicular bisector of a given line segment.
View SolutionDraw perpendicular bisector to line segment AB if l(AB)=7cm.
View SolutionIn the given figure, AB is a line segment. P and Q are points on opposite sides of AB such that each of them is equidistant from the points A and B. Show that the line PQ is the perpendicular bisector of AB.
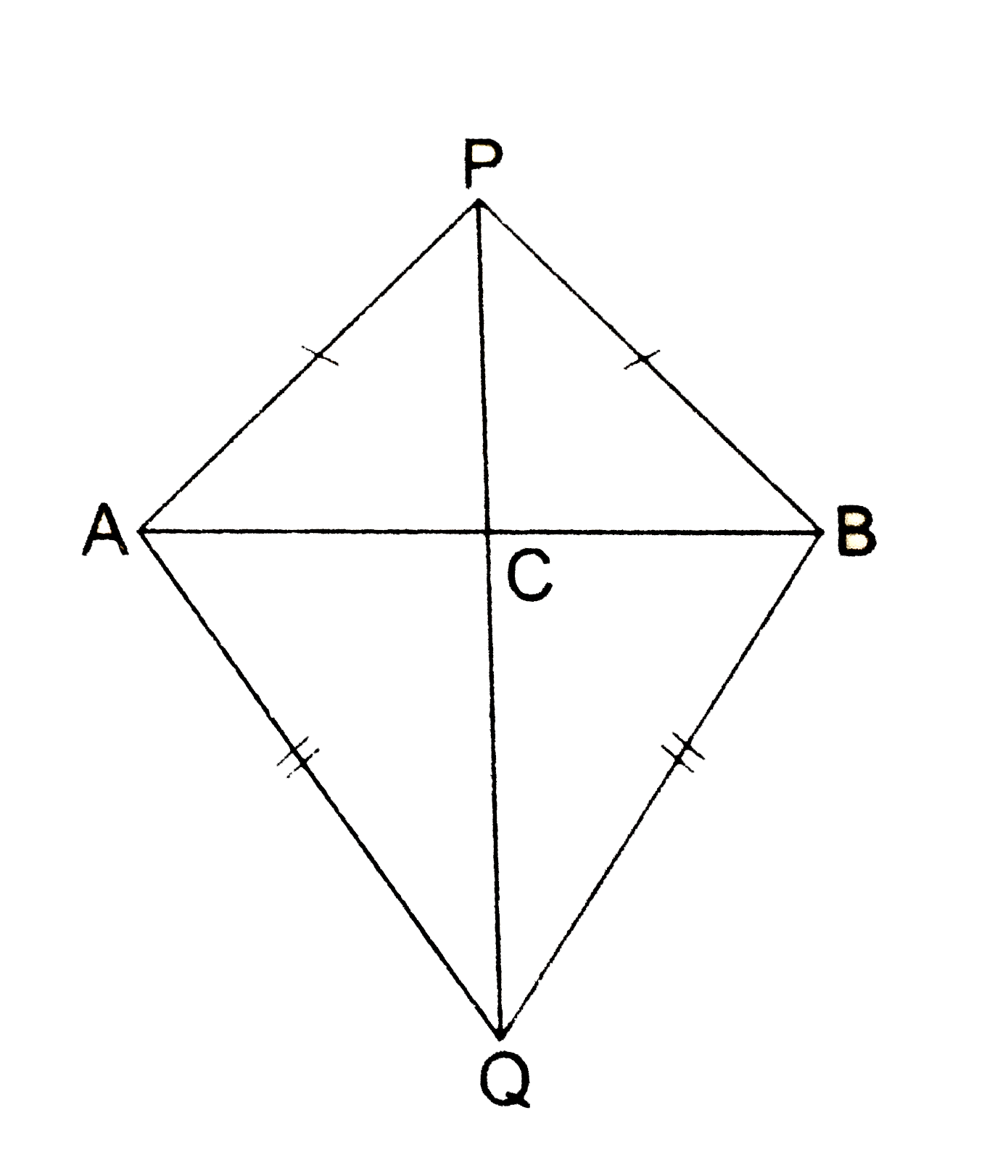
View SolutionAB is a line segment. P and Q are points on opposite sides of AB such that each of them is equidistant from the points A and B (in figure). Show that the line PQ is perpendicular bisector of AB
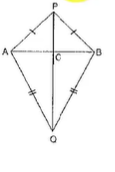
View SolutionTwo chords AB and CD of a circle are parallel and a line l is the perpendicular bisector of AB. Show that l bisects CD
View SolutionTwo chords AB and CD of a circle are parallel and a line l is the perpendicular bisector of AB . Show that l bisects CD.
View SolutionAB is a line-segment. P and Q are points on opposite sides of AB such that each of them is equidistant from the points A and B (see Fig. 7.37). Show that the line PQ is the perpendicular bisector of AB
View Solution
