In the given figure, AB is a line segment. P and Q are points on opposite sides of AB such that each of them is equidistant from the points A and B. Show that the line PQ is the perpendicular bisector of AB.
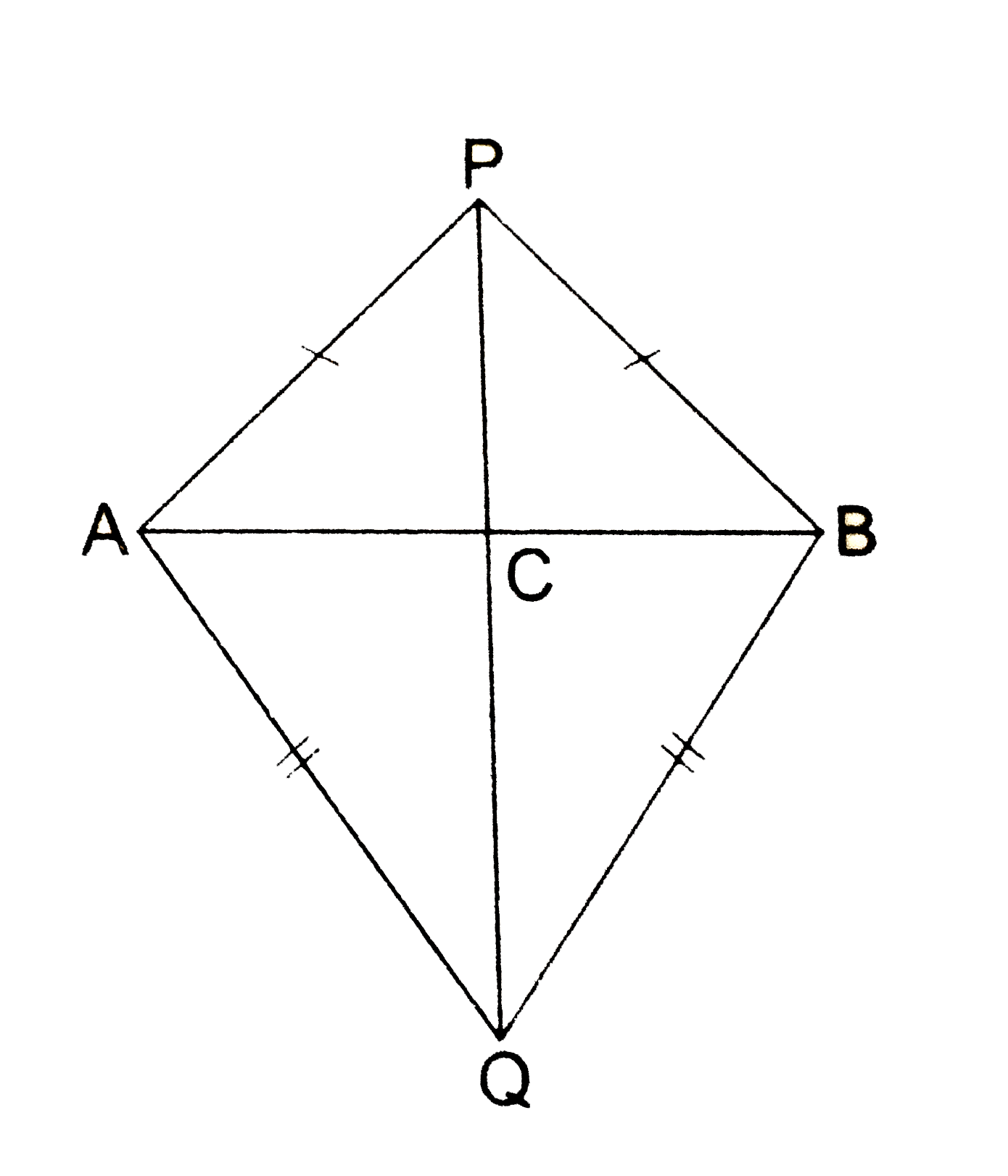
GIVEN A line segment AB and two point P and Q such that PA = PB and QA = QB.
TO PROVE Let AB and PQ intersect at C. Then, we have to prove that AC = BC and ∠ACP=90∘.
PROOF In ΔPAQandΔPBQ, we have
PA=PB (given)
OA=QB (given)
PQ=PQ (common)
∴ ΔPAQ≅ΔPBQ (by SSS-criteria).
∴ ∠APQ=∠BPQ ...(i) (c.p.c.t.).
Now, in ΔPACandΔPBC, we have
PA=PB (given)
∠APC=∠BPC [∵∠APQ=∠BPQ in (i)]
PC=PC (common)
∴ ΔPAC≅ΔPBC (by SAS-criteria).
∴ AC=BC ...(ii) (c.p.c.t.).
And, ∠ACP=∠BCP ...(iii) (c.p.c.t.).
But, ∠ACP+∠BCP=180∘ (linear pair).
∴ 2∠ACP=180∘ [using (iii)].
So, ∠ACP=90∘.
Hence, PQ is the perpendicular bisector of AB.
Topper's Solved these Questions
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Exercise 9A
27 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Exercise 9B
16 Videos
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - MULTIPLE CHOICE QUESTION(MCQ)
37 Videos
- COORDINATE GEOMETRYBOOK - RS AGGARWALCHAPTER - COORDINATE GEOMETRYEXERCISE - Multiple Choice Questions (Mcq)
22 Videos
Similar Questions
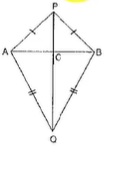
AB is a line-segment. P and Q are points on opposite sides of AB such that each of them is equidistant from the points A and B (see Fig. 7.37). Show that the line PQ is the perpendicular bisector of AB
View SolutionAB is a line segment. P and Q are points on opposite sides of AB such that each of them is equidistant from the points A and B (in figure). Show that the line PQ is perpendicular bisector of AB
View SolutionShow that the locus of a point, equidistant from the endpoints of a line segment, is the perpendicular bisector of the segment
View SolutionShow that the locus of a point, equidistant from the endpoints of a line segment, is the perpendicular bisector of the segment
View SolutionAB is a line segment and line l is its perpendicular bisector. If a point P lies on l, show that P is equidistant from A and B.
View SolutionAB is a line segment and line l is its perpendicular bisector. If a point P lies on l, show that P is equidistant from A and B.
View SolutionDraw a line segment AB=5.6cm. Draw the perpendicular bisector of AB.
View SolutionIn the given figure, P (4, 2) is mid-point of line segment AB. Find the co-ordinates of A and B.
View SolutionDraw a perpendicular bisector of line segment AB = 8cm.
View SolutionDraw a line segment AB of length 4.8 cm. Draw the perpendicular bisector of seg AB
View Solution
