AB is a line segment and line l is its perpendicular bisector. If a point P lies on l, show that P is equidistant from A and B.
To prove that point P, which lies on the perpendicular bisector of line segment AB, is equidistant from points A and B, we can follow these steps:
1. Identify the Elements:
- Let A and B be two points on a plane, and let C be the midpoint of line segment AB.
- Since line l is the perpendicular bisector of AB, it intersects AB at point C and forms right angles with it.
2. Draw the Perpendicular Bisector:
- Draw line segment AB and locate point C, which is the midpoint of AB.
- Draw line l such that it is perpendicular to AB at point C.
3. Place Point P:
- Let point P be any point on line l.
4. Consider Triangles PAC and PBC:
- We will consider triangles PAC and PBC to show that PA = PB.
5. Identify Common Sides:
- The segment PC is common to both triangles PAC and PBC.
6. Show Right Angles:
- Since line l is the perpendicular bisector, angle PCA = angle PCB = 90 degrees.
7. Show Equal Lengths:
- Since C is the midpoint of AB, we have AC = BC.
8. Apply the SAS Congruence Criterion:
- We have:
- PC = PC (common side)
- Angle PCA = Angle PCB = 90 degrees (right angles)
- AC = BC (since C is the midpoint)
- Therefore, by the Side-Angle-Side (SAS) criterion, triangles PAC and PBC are congruent.
9. Conclude Equidistance:
- By the property of congruent triangles, we have PA = PB.
- Thus, point P is equidistant from points A and B.
Conclusion:
Since we have shown that PA = PB, we conclude that point P is equidistant from points A and B.
---
- Let A and B be two points on a plane, and let C be the midpoint of line segment AB.
- Since line l is the perpendicular bisector of AB, it intersects AB at point C and forms right angles with it.
- Draw line segment AB and locate point C, which is the midpoint of AB.
- Draw line l such that it is perpendicular to AB at point C.
- Let point P be any point on line l.
- We will consider triangles PAC and PBC to show that PA = PB.
- The segment PC is common to both triangles PAC and PBC.
- Since line l is the perpendicular bisector, angle PCA = angle PCB = 90 degrees.
- Since C is the midpoint of AB, we have AC = BC.
- We have:
- PC = PC (common side)
- Angle PCA = Angle PCB = 90 degrees (right angles)
- AC = BC (since C is the midpoint)
- Therefore, by the Side-Angle-Side (SAS) criterion, triangles PAC and PBC are congruent.
- By the property of congruent triangles, we have PA = PB.
- Thus, point P is equidistant from points A and B.
Since we have shown that PA = PB, we conclude that point P is equidistant from points A and B.
Similar Questions
AB is a line segment and line l is its perpendicular bisector. If a point P lies on l, show that P is equidistant from A and B.
View SolutionA line segment is symmetrical about its perpendicular bisector.True or false?
View SolutionIn the given figure, AB is a line segment. P and Q are points on opposite sides of AB such that each of them is equidistant from the points A and B. Show that the line PQ is the perpendicular bisector of AB.
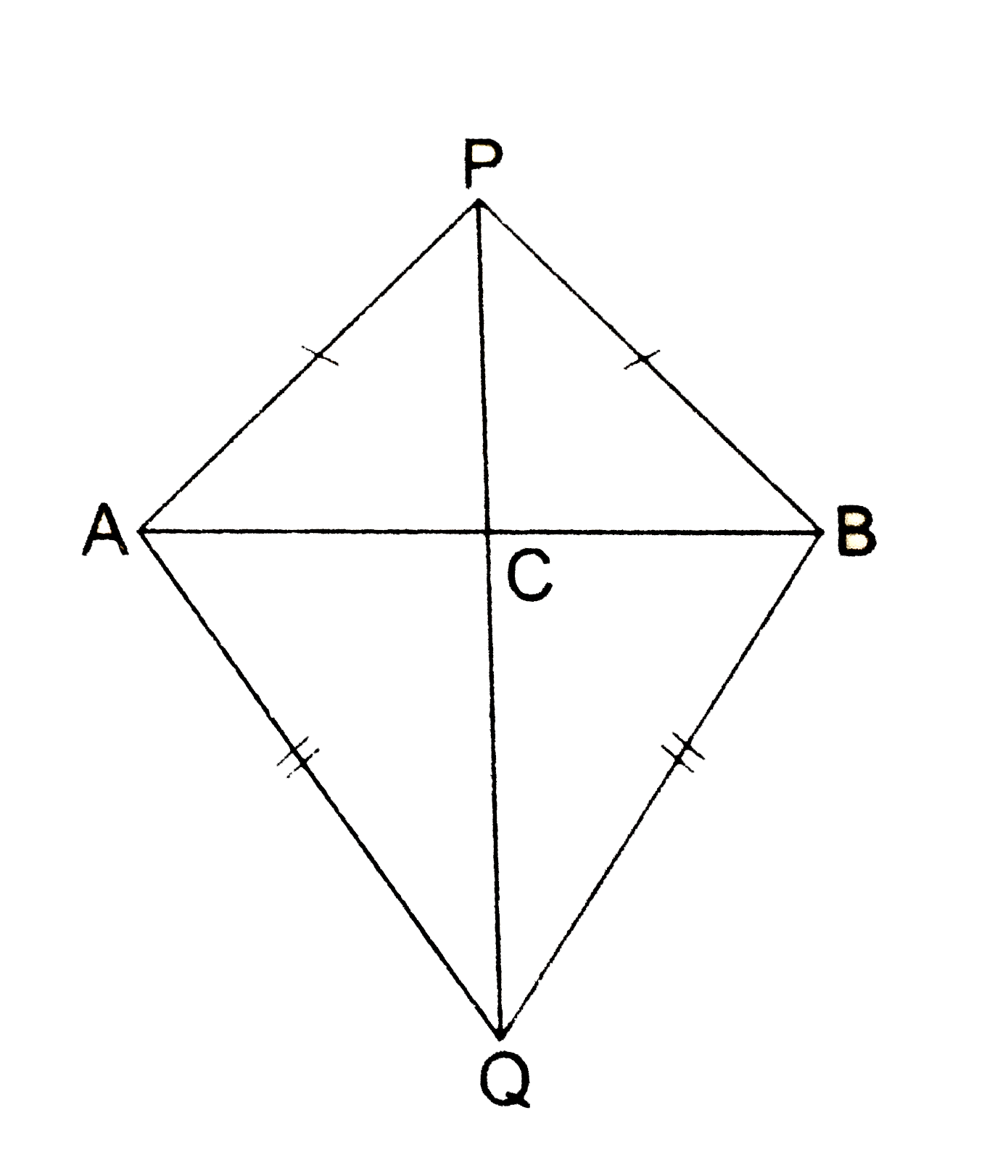
View SolutionAB is a line-segment. P and Q are points on opposite sides of AB such that each of them is equidistant from the points A and B (see Fig. 7.37). Show that the line PQ is the perpendicular bisector of AB
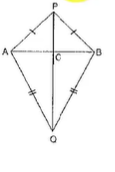
View SolutionAB is a line segment. P and Q are points on opposite sides of AB such that each of them is equidistant from the points A and B (in figure). Show that the line PQ is perpendicular bisector of AB
View SolutionDraw a perpendicular bisector of line segment AB = 8cm.
View SolutionDraw the perpendicular bisector of the line segment AB= 6 cm .
View SolutionDraw the perpendicular bisector of the line segment AB=5 cm.
View SolutionTwo lines l and m interset at the O and P is Point on a line n Passing through the point O such that P is equidistant from l and m. Prove that n is the bisectof the angle formed by l and m
View SolutionDraw the perpendicular bisector of the line segment AB= 6 cm .
View Solution
