Question

Show that the locus of a point, equidistant from the endpoints of a line segment, is the perpendicular bisector of the segment

Explanation

The proof will be taken up in two steps :
Step 1: We, initially prove tha tany point equidistant form the end point of a line segment lies on the perpendicular bisector of the line segment.
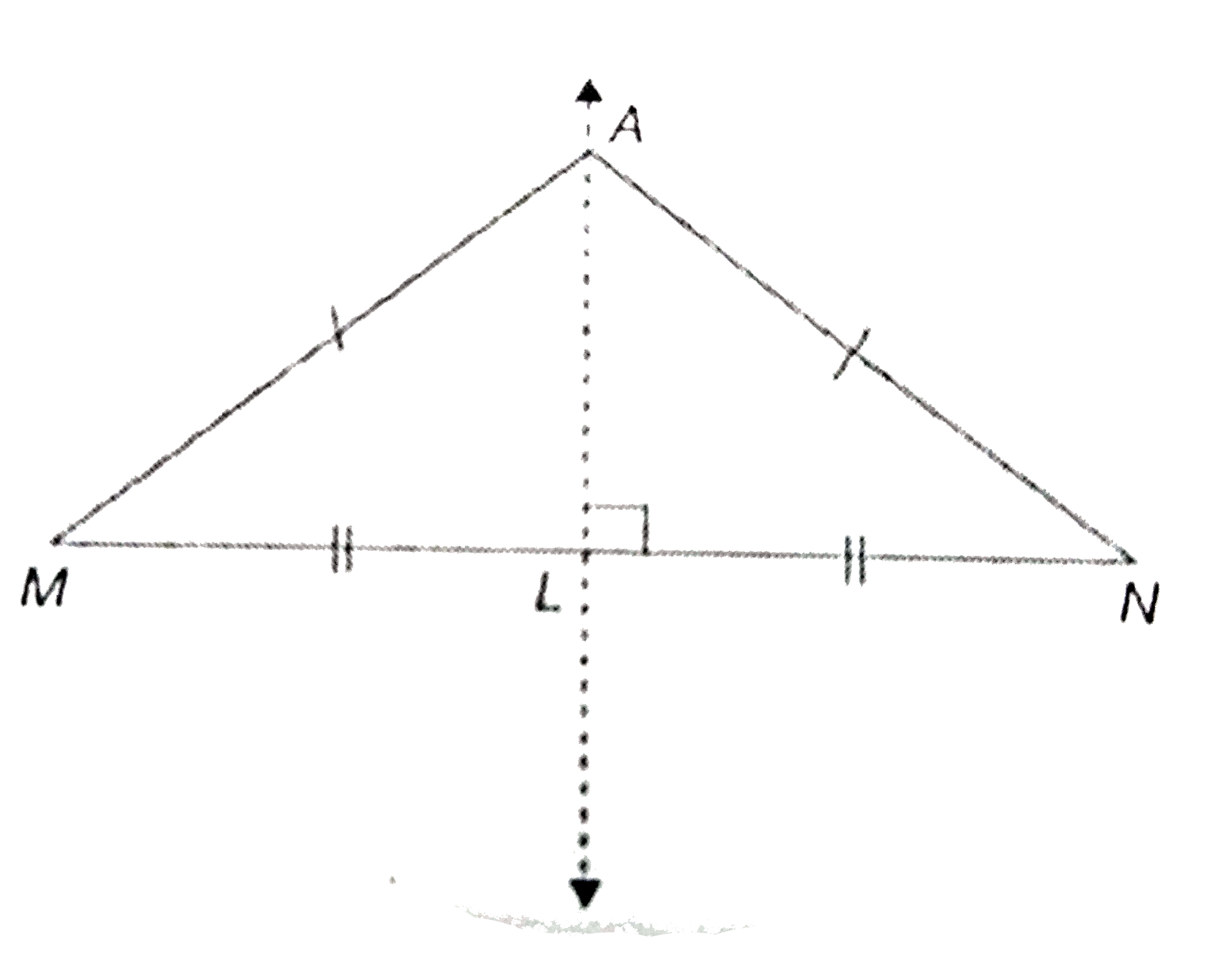
Given : M and N are two points on a plane. A is a point in the same plane such that `AM=AN`.
RTP: A lies on the perpendicular bisector of MN.
Proof : Let M and N be the two fixed points in a plane
Let A be a point such that `AM=AN` and L be the mid -points of `overline(MN)`.
If A coincides with L, then A lies on the bisector of MN. Suppose A is different from L.
Then, in `Delta MLA and Delta NLA`,
`ML=NL,AM=AN` and AL is a common side.
`therefore` By SSS congruence property, `Delta MLA approx Delta NLA`
`rArr angle MLA =angle NLA(because "Corresponding elements of congruent triangles are equal") (1)`
But `angle MLA +angle NLA =180^@(because "They form a straight angle")`
`rArr 2 angle MLA =180^@("using(1))`
`therefore angle MLA angle NLA =90^@`
So, `overline(AL) bot overline (MN)` and hence `overline(AL)` is the perpendicular bisector of `overline(MN)`.
`therefore` A lies on the perpendicular bisector of `overline(MN)`.
Step 2 : Now, we prove that any point of the line segment.
Given : MN is the segment and P is point on the perpendicular bisector. L is the mid-point of MN.
RTP : `MP=NP`
Proof : If P coincides with L, then MP=NP. Suppos P is different from L. Then, in `Delta MLP and NLP, ML=LN`
LP is the common side and `angle MLP=angle NLP=90^@`
`therefore` By the SAS congruence property , `Delta MLPapprox Delta NLP`.
So, `MP=PN` (`because` The corresponding bisector of `overline(MN)` is eqidistant from the points M and N .
Hence , from the steps 1 and 2 of the proof it can be said that the locus of the point equidistant from two fixed points is the perpendicular bisector of the line segment joining the two points.