Question

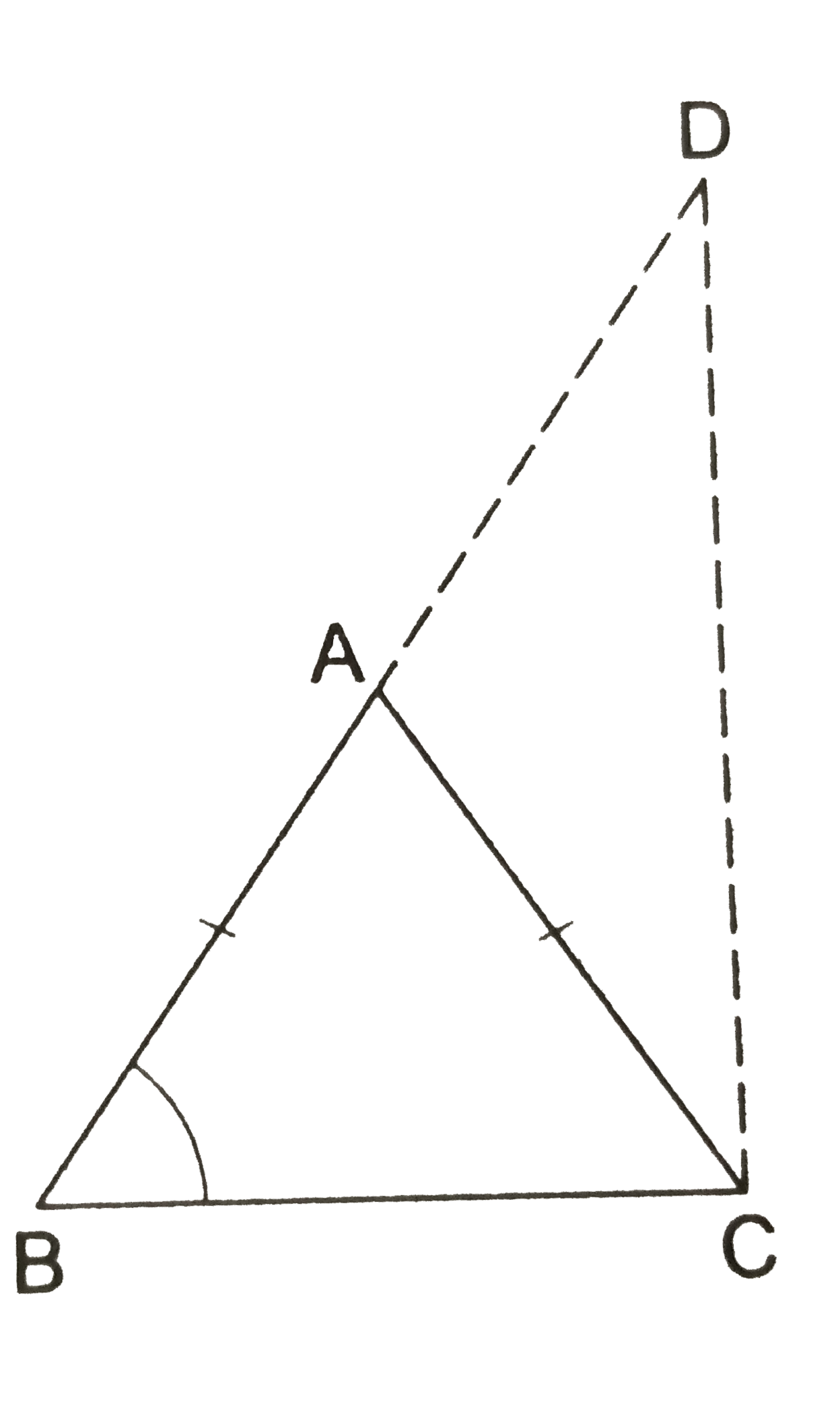
$\Delta ABC,AB=AC$ and BA is produced to D such that AC = AD. Then the $\angle BCD$ is

Options

A. `100^@`
B. `60^@`
C. `80^@`
D. `90^@`

Answer

D

Explanation

To solve the problem, we need to analyze the given triangle ABC where AB = AC and the line BA is extended to point D such that AC = AD. We need to find the measure of angle BCD.

1. Identify the Triangle and Given Information:
- We have triangle ABC where AB = AC.
- Point D is on the extension of line BA such that AC = AD.

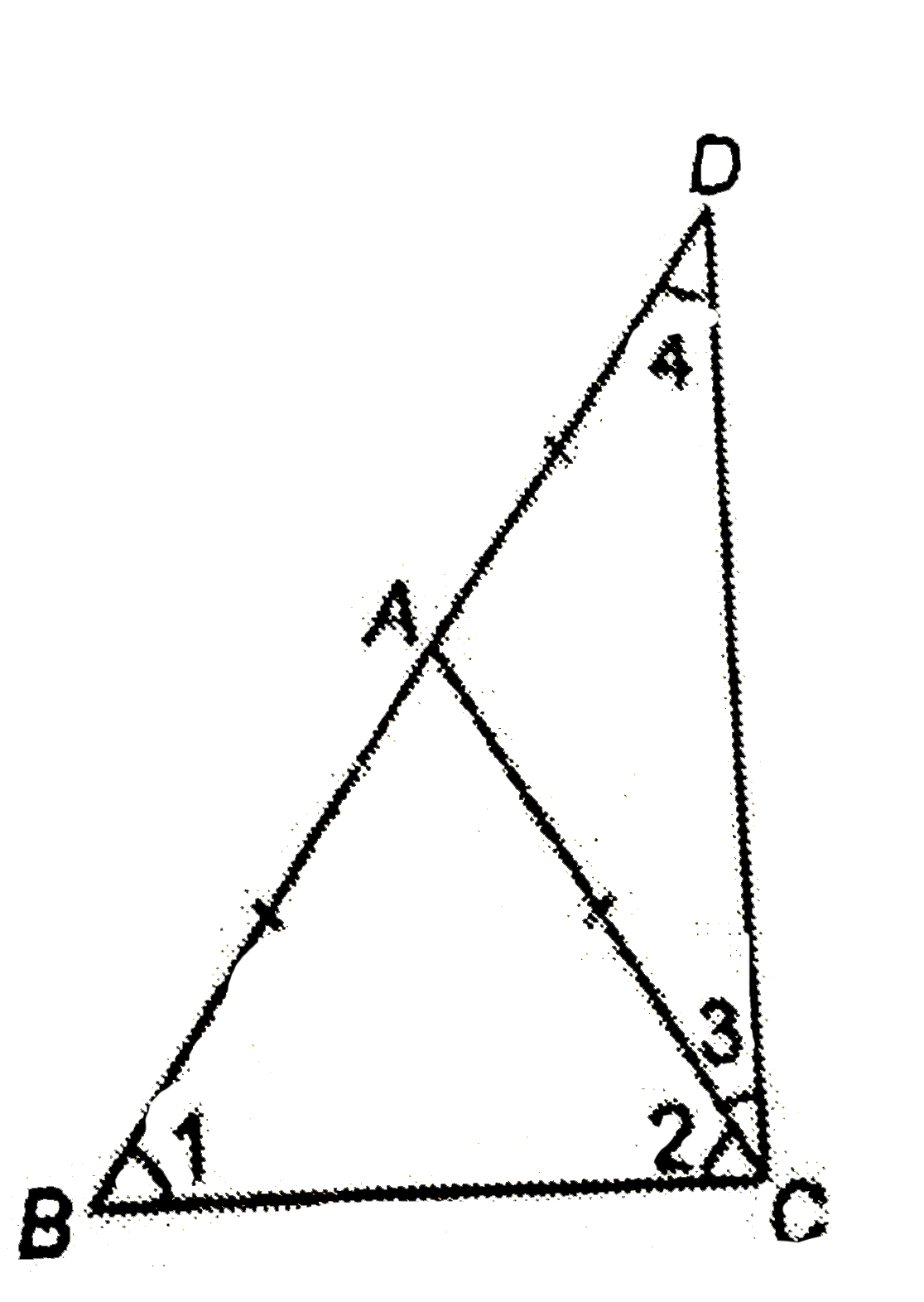
2. Label the Angles:
- Let angle ABC = x.
- Since AB = AC, by the properties of isosceles triangles, angle ACB = x as well.

3. Determine Angle A:
- The sum of angles in triangle ABC is 180 degrees:
\( \text{Angle A} + \text{Angle ABC} + \text{Angle ACB} = 180 \)
- Thus, we have:
\( \text{Angle A} + x + x = 180 \)
- This simplifies to:
\( \text{Angle A} + 2x = 180 \)
- Therefore:
\( \text{Angle A} = 180 - 2x \)

4. Analyze Triangle ACD:
- In triangle ACD, we know that AC = AD (given).
- Therefore, triangle ACD is also isosceles, which means:
\( \text{Angle ADC} = \text{Angle ACD} = y \)
- The sum of angles in triangle ACD is also 180 degrees:
\( \text{Angle A} + \text{Angle ADC} + \text{Angle ACD} = 180 \)
- This gives us:
\( (180 - 2x) + y + y = 180 \)
- Simplifying this, we find:
\( 180 - 2x + 2y = 180 \)
- Thus:
\( 2y = 2x \quad \Rightarrow \quad y = x \)

5. Find Angle BCD:
- In triangle BCD, we can express the angles as follows:
\( \text{Angle ABC} + \text{Angle BCD} + \text{Angle BDC} = 180 \)
- We know that angle BDC is equal to angle ADC, which we found to be y. Thus:
\( x + \text{Angle BCD} + y = 180 \)
- Since y = x, we can substitute:
\( x + \text{Angle BCD} + x = 180 \)
- This simplifies to:
\( 2x + \text{Angle BCD} = 180 \)
- Rearranging gives:
\( \text{Angle BCD} = 180 - 2x \)

6. Substituting for Angle BCD:
- We already established that angle A = 180 - 2x. Therefore:
\( \text{Angle BCD} = 90 \)

Conclusion:
The measure of angle BCD is 90 degrees.