Two monochromatic coherent sources of wavelength 5000 Å are placed along the line normal to the screen as shown in the figure.
(a) Determine the condition for maxima, at the point P.
(b)Find the order of the central bright fringe if d = 0.5 mm, D = 1 m.

The optical path difference at P is
P=S1P−S2P=dcosθ
Since cosθ=1−θ22, where θ is small,
Therefore p=d(1−θ22)
=d[1−y22D2]
For the maxima p=nλ
∴y=D√2(1−nλd)
(b) At the central maxima, θ=0
∴p=d=nλ
or n=dλ=0.50.5×10−3=1000

Topper's Solved these Questions
- OPTICSBook:FIITJEEChapter:OPTICSExercise:Solved problem (objective)
Explore 15 Videos
- OPTICSBook:FIITJEEChapter:OPTICSExercise:Comprehension-1(prob)
Explore 3 Videos
- OPTICSBook:FIITJEEChapter:OPTICSExercise:Illustration
Explore 10 Videos
- MODERN PHYSICSBook:FIITJEEChapter:MODERN PHYSICSExercise:Numerical based questions
Explore 5 Videos
- PHYSICS PART-IIIBook:FIITJEEChapter:PHYSICS PART-IIIExercise:NUMERICAL BASED QUESTIONS DECIMAL TYPE
Explore 11 Videos
Similar Questions
Light of wavelength 6000Å is incident on a slit of width 0.30 mm. The screen is placed 2 m from the slit. Find (a) the position of the first dark fringe and (b). The width of the central bright fringe.
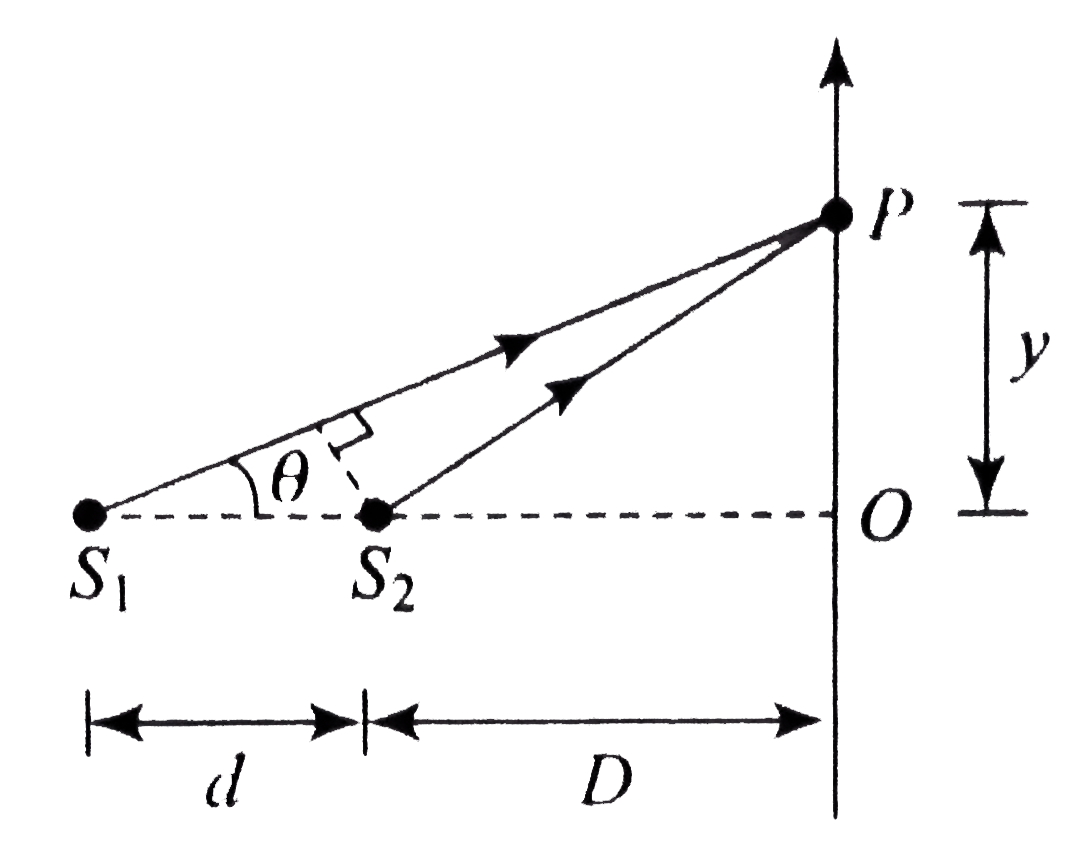
View SolutionIn the YDSE, the monochromatic source of wavelength λ is placed at a distance d2 from the central axis (as shown in the figure), where d is the separation between the two slits S1andS2 .
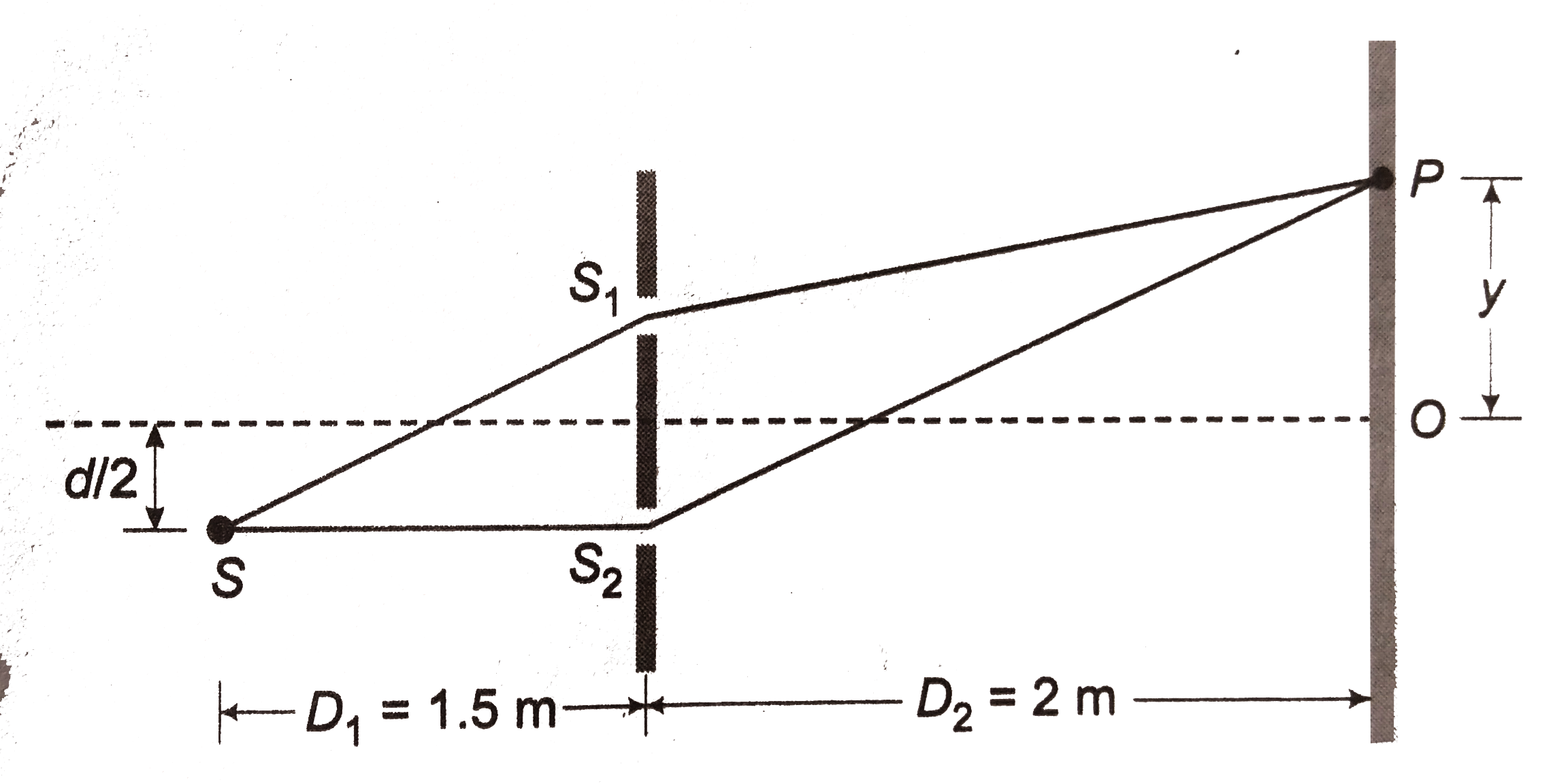
(a)Find the position of the central maxima.
(b) Find the order of interference formed at O.
(c)Now, S is placed on centre dotted line. Find the minimum thickness of the film of refractive indes μ=1.5 to be placed in front of S2 so that intensity at O becomes 34th of the maximum intensity.
(Take λ=6000Å,d=6mm.)
View Solution
Knowledge Check
Two coherent point sources S1 and S2 are separated by a small distance d as shown. The fringes obtained on the screen will be
 ApointsBstraight linesCsemi-circlesDconcentric circles
ApointsBstraight linesCsemi-circlesDconcentric circlesIn figure, a screen is placed normaol to the line joining the two point coherent sources S1 and S2. The interference pattern consists of concentric circles.
Find the radius of the nth bright ringAD√1(1−nλd)BD√2(1−nλd)C2D√2(1−nλd)DD√2(1−nλ2d)Two coherent point sources S1andS2 are separated by a small distance 'd' as shown. The fringes obtained on the screen will be :
 Astraigth linesBsemi-circleCconcentric circlesDpoints
Astraigth linesBsemi-circleCconcentric circlesDpoints
In the YDSE conducted with white light (4000Å-7000Å), consider a point P1onthescreenat y1 = 0.2mm. Determine the wavelengths which form maxima at these points :

View SolutionLight of wavelength 6000Å is incident normally on single slit of width 0.23 mm. Find the angular spread between the central maxima and second-order maxima of diffraction pattern.
View SolutionIn the figure shown, a screen is placed normal to the line joining the two point coherent sources S1andS2. The interference pattern consists of concentric circles.
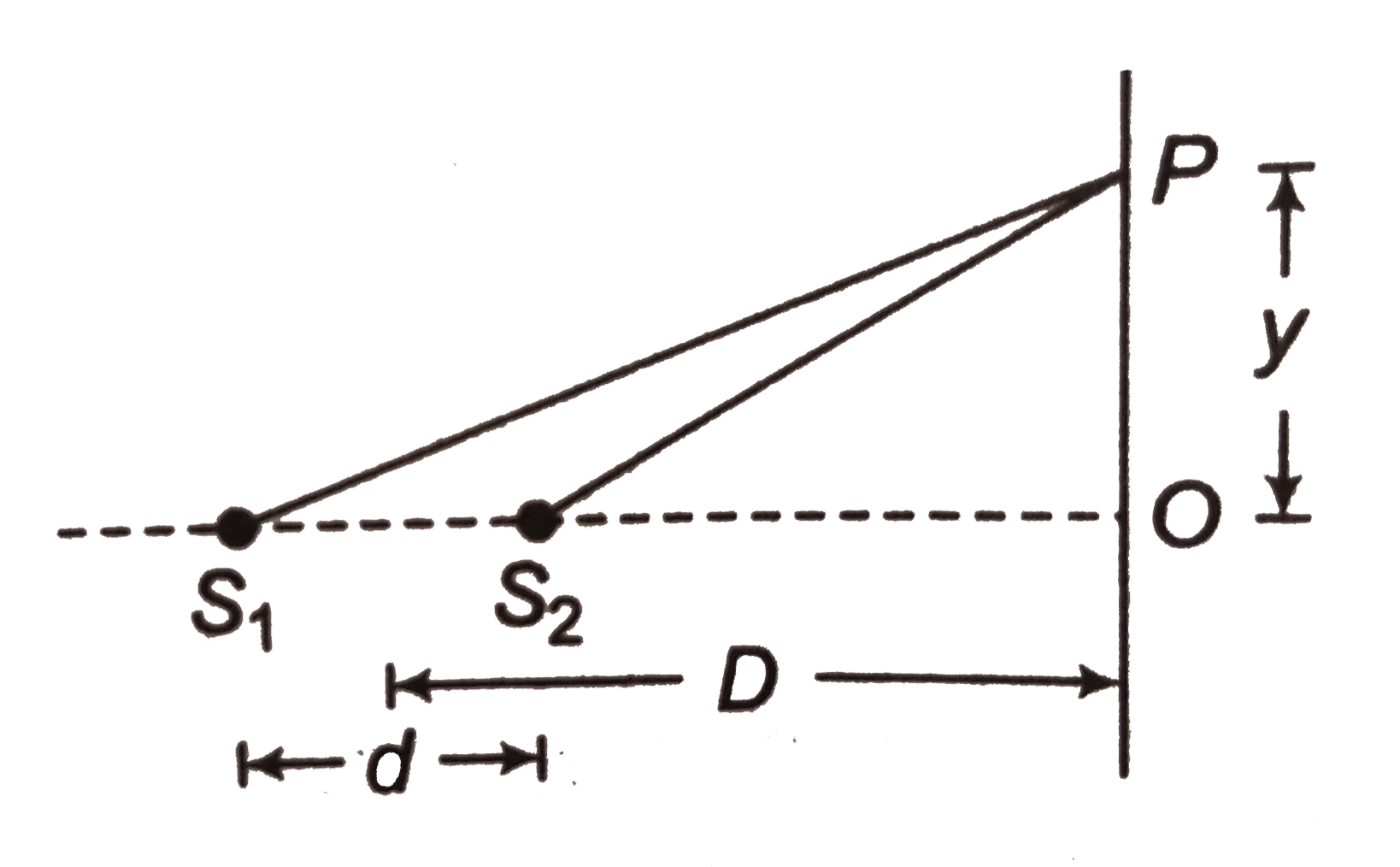
(a)Find the radius of the nth bright ring.
(b) If d=0.5 mm, λ=5000Å and D=100 cm, find the radius of the closest second bright ring.
(c) Also, find the value of n for this ring.
View SolutionAssertion: Two coherent sources S1andS2 are placed in front of a screen as shown in figure. At point P, 10th order maxima is obtained. Then , 11th order maxima will be obtained above P.

Reason: For 11th order maxima path difference should be more.
View SolutionFringes are produced with monochromatic light of wavelength 5500 Å. A thin glass plate of R.I. 1.5 is then placed normally in one of the paths of interfering beams and the central bright fringe is found to be shifted to the position, previously occupied by the third bright band from the centre. the thickness of the glass plate is
View Solution