A hemisphere of radius R, made of glass of refractive index (3/2) is placed on 'the table. A point source of light is placed at a distance 2R from the centre, of hemisphere. If source is viewed diametrically opposite side of hemisphere. Find the position of image of source.

Refraction due to first surface.
Refraction due to second surface.
Position of image from the centre of hemisphere is at a distance 6R opposite side of source.
Topper's Solved these Questions
- OPTICSBook:FIITJEEChapter:OPTICSExercise:Solved problem (objective)
Explore 15 Videos
- OPTICSBook:FIITJEEChapter:OPTICSExercise:Comprehension-1(prob)
Explore 3 Videos
- OPTICSBook:FIITJEEChapter:OPTICSExercise:Illustration
Explore 10 Videos
- MODERN PHYSICSBook:FIITJEEChapter:MODERN PHYSICSExercise:Numerical based questions
Explore 5 Videos
- PHYSICS PART-IIIBook:FIITJEEChapter:PHYSICS PART-IIIExercise:NUMERICAL BASED QUESTIONS DECIMAL TYPE
Explore 11 Videos
Similar Questions
A point source of light is placed at a distance of 2f from a converging lens of focal length f. The intensity on the other side of the lens is maximum at a distance
View SolutionA point light source of 100W is placed at a distance x from the centre ofa hole ofradius R in a sheet as shown in figure, Find the power passing through the hole in sheet

View Solution
Knowledge Check
A glass hemisphere of radius R and of material having refractive index 1.5 is silvered on its flat face as shown in figure., A small object of height h is located at a distance 2R from the surface of hemisphere as shown in the figure. The final image will form.
 Aat a distance of Rfrom silvered surface, on the right side.Bon the object itselfCat hemispher surfaceDat a distance of 2R from the silvered surface, on left side
Aat a distance of Rfrom silvered surface, on the right side.Bon the object itselfCat hemispher surfaceDat a distance of 2R from the silvered surface, on left sideThe distance of the centre of mass of a hemispherical shell of radius R from its centre is
AR2BR3C2R2D2R3
A solid glass sphere with radius R and an index of refraction 1.5 is silvered over one hemisphere. A small object is located on the axis of the sphere at a distance 2R to the left of the vertex of the unsilvered hemisphere. Find the position of final image after all refractions and reflection have taken place.
View SolutionThe internal surface of the walls of a sphere is specular (i.e. reflecting). The radius of the sphere is R=36cm. A point source S is placed at a distance R/2 from the centre of the sphere and sends light to the remote part of the sphere. Where will the image of the source be after two successive reflection from the remote and then the nearest wall of the sphere ? How wil the position of the image change if the source sends light to the nearest wall first ? Consider paraxial rays.
View SolutionThere is a hemisphere whose radius of curvature is r and inner side of it is made completely reflecting . A point source of light of power P is kept at the centre of curvature of hemisphere . Calculate the force exerted by the light falling on inner side of hemispherical surface.
View SolutionThe inner surface of the wall of a sphere is perfectly reflecting. Radius of the sphere is R. A point source S is placed at a distance R/2 from the centre of the sphere. Consider the reflection of light from the farthest wall followed by reflection from the nearest wall. Where is the image of the source? Consider paraxial rays only.
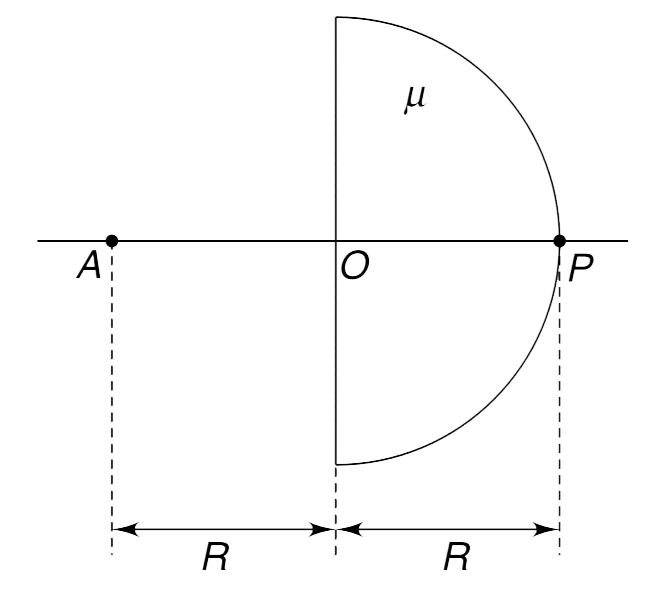
View SolutionA point source (A) is kept on the axis of a hemi- spherical paperweight made of glass of refractive indexμ=32 . The distance of the point source from the centre (O) of the sphere is R where R is radius of the hemisphere. Use paraxial approximations for answering following questions (a) Find the change in radius of curvature of the wave- fronts just after they enter the glass at O. (b) Find the radius of curvature of the wavefronts at point P just outside the glass.
View SolutionThe internal surface of the walls of a sphere is specular. The radius of the sphere is R=36cm. A point source S is placed at a distance R/2 from the cneter of the sphere and sends light to the remote part of the sphere. Where will the image of the source be after two successive reflections from the remote and then nearest wall of the sphere? How will the position of the image change if the source sends light to the nearest wall first?Consider paraxial rays.
View Solution
