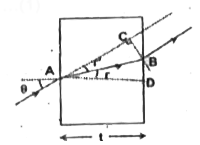
A ray of light strikes a glass slab of thickness t.
(i) Prove that it emerges on the opposite face, parallel to the initial ray.
(ii) (ii) Prove that the value of deflection of beam which passed through the plate is :
(iii) Prove that for a small angle of incidence , the internal shift x is given by
where is the refractive index of glass with respect to air.
Lateral shift,
…(2)
where AB= t/cosr and r= angle of refraction given by using snell.s law,
& cosr in (1) we obtain
(b) If is small, can be ignored in comparison to 1,
Topper's Solved these Questions
- OPTICSBook:FIITJEEChapter:OPTICSExercise:Solved problem (objective)
Explore 15 Videos
- OPTICSBook:FIITJEEChapter:OPTICSExercise:Comprehension-1(prob)
Explore 3 Videos
- OPTICSBook:FIITJEEChapter:OPTICSExercise:Illustration
Explore 10 Videos
- MODERN PHYSICSBook:FIITJEEChapter:MODERN PHYSICSExercise:Numerical based questions
Explore 5 Videos
- PHYSICS PART-IIIBook:FIITJEEChapter:PHYSICS PART-IIIExercise:NUMERICAL BASED QUESTIONS DECIMAL TYPE
Explore 11 Videos
Similar Questions
Knowledge Check
A ray of light strikes a glass slab of thickness t. It emergens on the opposite face, parallel to the incident ray but laterally displaced. The lateral displacement, Δx is
AΔx=0BΔx = t sin ( I - r) cos rCΔx=t sin Icos rDΔx= t sin ( I - r)cos rA ray of light strikes a glass slab (R.l. = μ) of finite thickness t. The emerging light is
Aparallel to. the incident rayBperpendicular to the incident rayCrotates by an angle[sin−1(1μ)]Dtotally internally reflectedA ray of light is incident on a glass slab of thickness t, at an angle i,r is the angle of refraction in the glass slab. Distance travelled in the glass slab is
AtcosrBanrCtcosrDtsinr
A ray of light passes from glass (μg=1.52) to water (μw=1.33). What is the critical angle of incidence?
View SolutionA ray of light passes through an equilateral glass prism such that the refracted ray inside the prism is parallel to its base. How is the angle of emergence i2 related to the angle of incidence i1.
View SolutionA light ray is incident on a plane glass slab of thickness ‘t’ at an angle of incidence ‘i’ as shown in the figure. If μ is the refractive index of glass. Then find time taken by the light ray to travel through the slab.
View SolutionA ray of light passes throught a plane glass slab of thickness t and refractive index μ=1.5. The angle between incident ray and emergent ray will be
View SolutionA ray of light is incident at the glass-water interface at an angle I, it emerges fimally parallel to the surface of water, the the value of μg would be
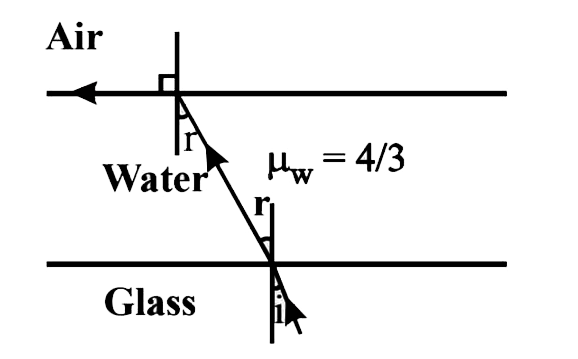
View Solution



