A biconvex lens of radii of curvature 20 cm has refractive index 1.56 for blue colour and 1.48 for red colour. The approximate linear spread of focus for white light is
3.6 cm
4.2 cm
3.0 cm
5.0 cm
The correct Answer is:C
To solve the problem of finding the approximate linear spread of focus for white light using a biconvex lens, we will follow these steps:
Step 1: Understand the Lens Formula
The lens formula for a biconvex lens is given by:
1f=(μ−1)(1R1−1R2)
For a biconvex lens, both radii of curvature (R1 and R2) are equal in magnitude but opposite in sign. Thus, if we denote the radius of curvature as R:
- R1=+R
- R2=−R
Step 2: Substitute Values into the Lens Formula
Substituting the values into the lens formula:
1f=(μ−1)(1R−1−R)=(μ−1)(1R+1R)=(μ−1)(2R)
Thus, we can express the focal length f as:
f=R2(μ−1)
Step 3: Calculate Focal Length for Blue and Red Light
Given:
- R=20cm
- μblue=1.56
- μred=1.48
Now, calculate the focal lengths for blue and red light:
1. For blue light:
fblue=202(1.56−1)=202(0.56)=201.12≈17.86cm
2. For red light:
fred=202(1.48−1)=202(0.48)=200.96≈20.83cm
Step 4: Calculate the Difference in Focal Lengths
Next, we find the difference in focal lengths:
Δf=fred−fblue≈20.83−17.86≈2.97cm≈3cm
Step 5: Conclusion
The approximate linear spread of focus for white light is:
Δf≈3cm
The lens formula for a biconvex lens is given by:
1f=(μ−1)(1R1−1R2)
For a biconvex lens, both radii of curvature (R1 and R2) are equal in magnitude but opposite in sign. Thus, if we denote the radius of curvature as R:
- R1=+R
- R2=−R
Substituting the values into the lens formula:
1f=(μ−1)(1R−1−R)=(μ−1)(1R+1R)=(μ−1)(2R)
Thus, we can express the focal length f as:
f=R2(μ−1)
Given:
- R=20cm
- μblue=1.56
- μred=1.48
1. For blue light:
fblue=202(1.56−1)=202(0.56)=201.12≈17.86cm
fred=202(1.48−1)=202(0.48)=200.96≈20.83cm
Next, we find the difference in focal lengths:
Δf=fred−fblue≈20.83−17.86≈2.97cm≈3cm
The approximate linear spread of focus for white light is:
Δf≈3cm
Topper's Solved these Questions
- OPTICSBook:FIITJEEChapter:OPTICSExercise:Comprehension-1(prob)
Explore 3 Videos
- OPTICSBook:FIITJEEChapter:OPTICSExercise:Comprehension-2(prob)
Explore 3 Videos
- OPTICSBook:FIITJEEChapter:OPTICSExercise:SOLVED PROBLEMS (SUBJECTIVE)
Explore 18 Videos
- MODERN PHYSICSBook:FIITJEEChapter:MODERN PHYSICSExercise:Numerical based questions
Explore 5 Videos
- PHYSICS PART-IIIBook:FIITJEEChapter:PHYSICS PART-IIIExercise:NUMERICAL BASED QUESTIONS DECIMAL TYPE
Explore 11 Videos
Similar Questions
A ray of light enters a spherical drop of water of refractive index μ as shown in figure.
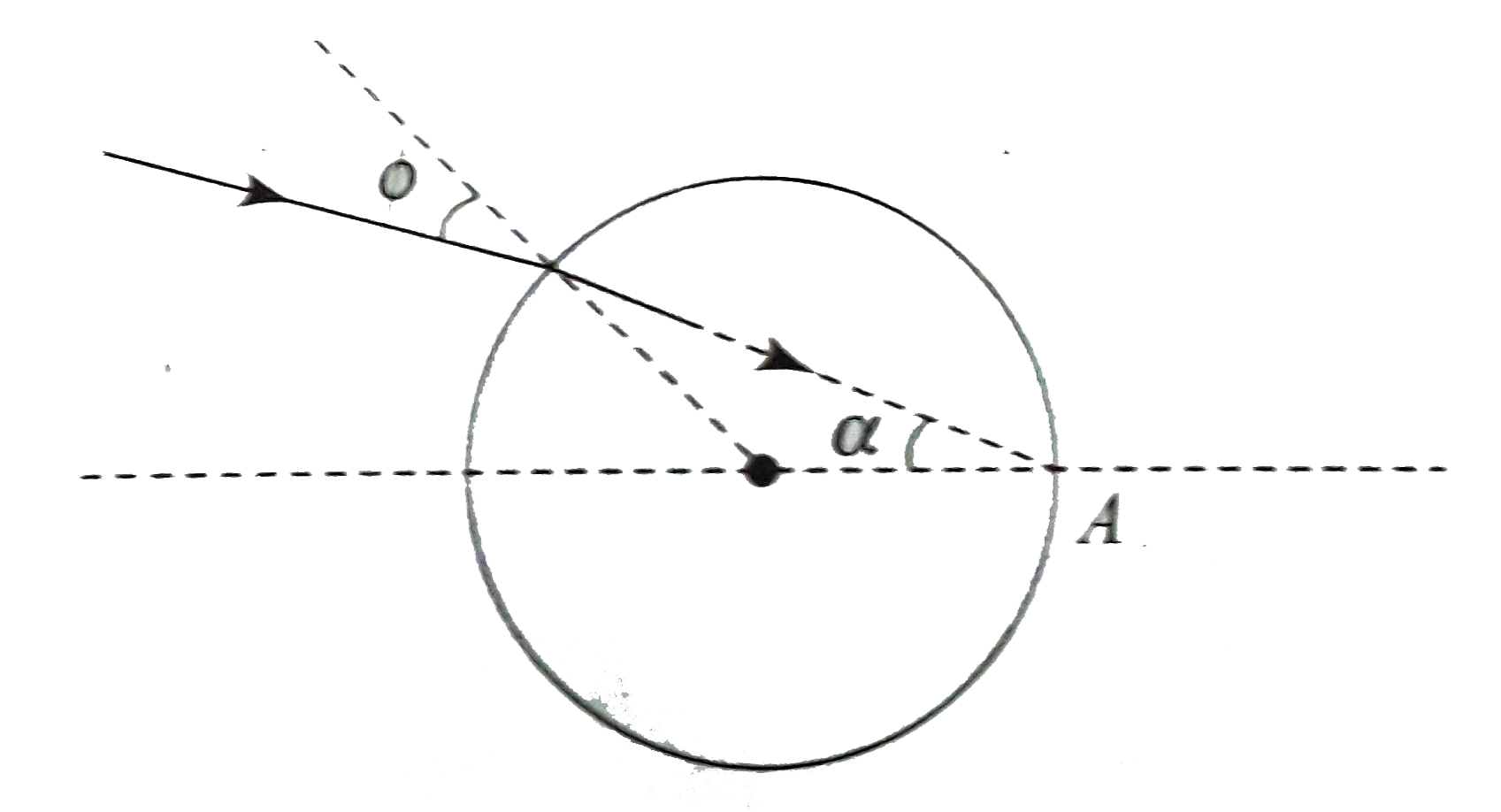
Q. Select the correct statement:
View SolutionA thin film of a specific meterial can be used to decrease the intensity of reflected light. There is destrucive inteference of wave reflected from upper and lower surface of the film. These films are called non-reflecting or anti-reflecting coatings. The process of coating the lens or surface with non-reflecting film is called blooming as shown in figure The refracting index of coating (n1) is less than that of the glass (n2).

4. If a light of wavelength λ is incident normally and the thickness of film is t, then optical path difference between waves reflected from upper and lower surface of the film is
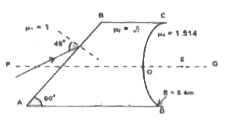
View SolutionA light ray is incident on an irregular shaped slab of refractive index √2 at an angle of 45∘with the normal on the incline face as shown in the figure. The ray finally emerges from the curved surface in the medium of the refractive index μ=1.514 and passes through point E. If the radius of curved surface is equal to 0.4 m. find the distance OE correct upto two decimal places.
View SolutionPhotons with energy 5eV are incident on a cathode C in a photoelectric cell . The maximum energy of emitted photoelectrons is 2eV. When photons of energy 6eV are incident on C , no photoelectrons will reach the anode A , if the stopping potential of A relative to C is
View SolutionThe range for a projectile that lands at the same elevation from which it is fired is given by R=(u2/g)sin2θ . Assume that the angle of projection = 30∘. If the initial speed of projection is increased by 1% , while the angle of projection is decreased by 2% . Then by what percentage does the range change ?
View Solutionएक उभयोत्तल लेन्स की दोनों वक्रता-त्रिज्याएँ 20 सेमी है तथा लेन्स के काँच का अपवर्तनांक 1.5 है | लेन्स की फोकस-दूरी होगी :
View Solutionएक उभयोत्तल लेंस की दोनों वक्रता-त्रिज्याएँ 20 सेमी है तथा लेंस की काँच का अपवर्तनांक 1.5 हैं | लेंस की फोकस-दुरी क्या होगी ?
View Solutionएक उभयोत्तल लेन्स की दोनों वक्रता त्रिज्याये 30 सेमी है तथा लेन्स के काँच का अपवर्तनांक 1.5 है। लेन्स की फोकस दूरी होगी-
View Solutionकाँच के बने द्विउत्तल लेंस की वक्रता-त्रिज्याएँ 15 cm तथा 20 cm हैं। लेंस की फोकस-दुरी निकले। (काँच का अपवर्तनांक= 1.5)
View Solutionकिसी उभयोत्तल लेंस के दो फलकों की वक्रता त्रिज्या 10 सेमी. तथा 15 सेमी. है। इसकी फोकस दूरी 12 सेमी. है। लेंस के काँच का अपवर्तनांक ज्ञात कीजिए।
View Solutionएक उत्तल लेंस की दोनों सतहों की वक्रता त्रिज्या 15 सेमी और 20 सेमी है। उसके पदार्थ का अपवर्तनांक 1.5 है। लेंस की फोकस-दूरी ज्ञात कीजिए।
View Solutionएक द्विअवतल लेंस के प्रत्येक पृष्ठ की वक्रता त्रिज्या 20 सेमी है तथा इसके पदार्थ का अपवर्तनांक 5/3 है | लेंस की फोकस दुरी ज्ञात कीजिए |
View Solutionएक द्विउत्तल लेंस के गोलीय पृष्ठों की वक्रता त्रिज्याएँ 20 सेमी तथा 30 सेमी है | लेंस के पदार्थ का वायु के सापेक्ष अपवर्तनांक 1⋅65 है | यदि लेंस को वायु के सापेक्ष अपवर्तनांक 1⋅1 के द्रव में डुबाकर रखा जाए, तो उसकी प्रभावी फोकस दुरी की गणना कीजिए |
View Solutionएक पतले उत्तल लेंस की वक्रता त्रिज्याएँ 20 सेमी तथा 30 सेमी है तथा पदार्थ का अपवर्तनांक 1⋅5 है | इसकी फोकस दुरी लगभग होंगी :
View Solutionकिसी काँच के उभयोत्तल लेंस के पृष्ठों की वक्रता त्रिज्याएँ क्रमश: 20 cm एवं 30 cm है। काँच का अपवर्तनांक 1.5 है। लेंस की फोकस दुरी ज्ञात कीजिये।
View Solutionकिसी 20 cm फोकस दुरी वाले काँच के उत्तल लेंस के पृष्ठों की वक्रता त्रिज्याएँ क्रमश: 18 cm एवं 24 cm है| लेंस के काँच का अपवर्तनांक ज्ञात कीजिए|
View Solution

