A biconvex lens has a refractive index of 1.5. The parallel beam of light incident on it forms an image at a distance of 12 cm. Calculate the radii of curvature of both the surfaces if the ratio of the radii of curvature is 2:3.
To solve the problem step-by-step, we will use the lens maker's formula and the given information about the lens.
Step 1: Understand the given information
We have a biconvex lens with:
- Refractive index (μ) = 1.5
- Image distance (focal length, f) = 12 cm (since parallel rays converge at the focal point)
- Ratio of the radii of curvature (R1:R2) = 2:3
Step 2: Use the lens maker's formula
The lens maker's formula for a biconvex lens is given by:
1f=(μ−1)(1R1−1R2)
Substituting the values we know:
112=(1.5−1)(1R1−1R2)
This simplifies to:
112=0.5(1R1−1R2)
Step 3: Substitute R2 in terms of R1
From the ratio of the radii of curvature, we can express R2 in terms of R1:
R1R2=23⟹R2=32R1
Step 4: Substitute R2 into the lens maker's formula
Now we substitute R2 in the lens maker's formula:
112=0.5⎛⎝1R1−132R1⎞⎠
This simplifies to:
112=0.5(1R1−23R1)
Combining the fractions:
1R1−23R1=3−23R1=13R1
Thus, we have:
112=0.5⋅13R1
This simplifies to:
112=16R1
Step 5: Solve for R1
Cross-multiplying gives:
6R1=12⟹R1=2 cm
Step 6: Calculate R2
Now, using the relationship R2=32R1:
R2=32×2=3 cm
Final Answer
The radii of curvature are:
- R1 = 10 cm
- R2 = 15 cm
We have a biconvex lens with:
- Refractive index (μ) = 1.5
- Image distance (focal length, f) = 12 cm (since parallel rays converge at the focal point)
- Ratio of the radii of curvature (R1:R2) = 2:3
The lens maker's formula for a biconvex lens is given by:
1f=(μ−1)(1R1−1R2)
Substituting the values we know:
112=(1.5−1)(1R1−1R2)
This simplifies to:
112=0.5(1R1−1R2)
From the ratio of the radii of curvature, we can express R2 in terms of R1:
R1R2=23⟹R2=32R1
Now we substitute R2 in the lens maker's formula:
112=0.5⎛⎝1R1−132R1⎞⎠
This simplifies to:
112=0.5(1R1−23R1)
Combining the fractions:
1R1−23R1=3−23R1=13R1
Thus, we have:
112=0.5⋅13R1
This simplifies to:
112=16R1
Cross-multiplying gives:
6R1=12⟹R1=2 cm
Now, using the relationship R2=32R1:
R2=32×2=3 cm
The radii of curvature are:
- R1 = 10 cm
- R2 = 15 cm
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - PRACTICE PROBLEMS (7)
12 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - PRACTICE PROBLEMS (8)
6 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - PRACTICE PROBLEMS (5)
3 Videos
- NUCLEIBOOK - MODERN PUBLICATIONCHAPTER - NUCLEIEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
15 Videos
- SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS BOOK - MODERN PUBLICATIONCHAPTER - SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS EXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
12 Videos
Similar Questions
A lens is 5cm thick and the radii of curvature of its object is placed at a distance of 12cm from the surface whose radius of curvature is 10cm. How far beyond the other surface is the image formed?
View SolutionThe radii of curvatureof double convex lens of glass (μ=1.5) are in the ratio of 1:2. This lens renders the rays parallel coming from an illuminated filament at a distance of 6cm. Calculate the radii of curvature of its surfaces.
View Solution
Knowledge Check
The focal length of a biconvex lens is 20 cm and its refractive index is 1.5. If the radii of curvatures of two surfaces of lens are in the ratio 1:2, then the larger radius of curvature is (in cm)
A10B15C20D30The power of a biconvex lens is 10 dioptre and the radius of curvature of each surface is 10 cm. Then the refractive index of the material of the lens is
A3/2B4/3C9/8D5/3A convex lens of refractive index 1.5 is given. It also has the radius of curvature of both the surfaces as 40 cm. Using this data, calculate the power of this lens.
A2.5 DBB 2DC1.5 DD1D
A biconvex lens has a focal length half the radius of curvature of either surface. What is the refractive index of lens material ?
View SolutionA double convex lens of glass (μ=1.5) renders parallel rays coming from a distant source at a distance of 5 cm. If the radii of curvature are in the ratio 1:2, calculate their individual values.
View SolutionA double convex lens made of glass of refractive index 1.56 has both radii of curvature of magnitude 20cm. If an object is placed at a distance of 10cm from this lens, find the position of image formed.
View SolutionThe refractive index of the material of a double convex lens is 1.5 and its focal length is 5cm .If the radii of curvature are equal the value of the radius of curvature ( in cms ) is
View SolutionA biconvex lens separates two media of refractive indices 1.3 and 1.7. the refractive index of the lens is 1.5 and the radii of curvature of the two sides of the lens are r1=10cm and r2=60cm .
The medium of refractive index 1.3 extends to 78 cm from the lens and that of refractive index 1.7 extends of 34 cm from the lens. A luminous object O is at a distance of 144 cm from the lens. Find the position of the final image from the lens.
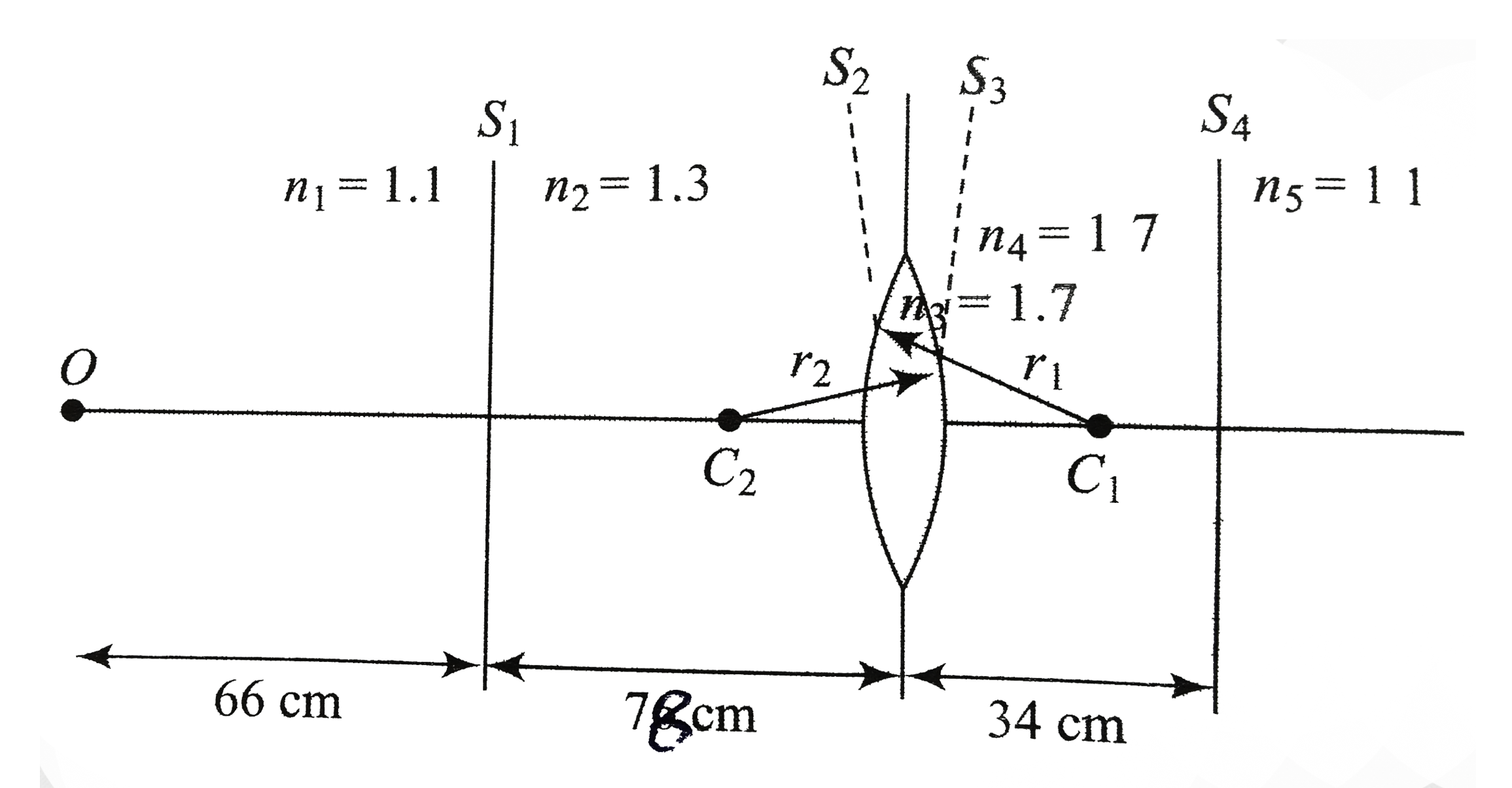
View Solution
