A beaker containing liquid is placed on a table, underneath a microscope which can be moved along a vertical scale. The microscope is focused, through the liquid onto a mark on the table when the reading on the scale is a. It is next focused on the upper surface of the liquid and the reading is b. More liquid is added and the observations are repeated, the corresponding readings are c and d. The refractive index of the liquid is

A

d−bd−c−b+a

B

b−dd−c−b+a

C

d−c−−b+d−b

D

d−ba+b−c−d

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:A

The real depth = (R.l.) apparent depth
⇒ In first case, the real depth ht = n(b-a)
Similarly in the second case,- the real depth h2 =? n (d-c)
Since. h2 > h, the difference of real depths = h2 - hi = n (d-c-b+a).
Since the liquid is added in second case, h2 - h! = d-b
⇒n=(d−bd−c−b+a)
Hence (A) is correct.

Updated on:21/07/2023
|
Class 12PHYSICSGEOMETRICAL OPTICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • If the surface of a liquid is plane, then the angle of contact of the liquid with the walls of container is

    Aacute angle
    Bobtuse angle
    C90∘
    D0∘

  • If the surface of a liquid is plane, then the angle of contact of the liquid with the walls of container is

    AAcute angle
    Bobtuse angle
    C90∘
    D0∘

  • A container filled with a liquid A is floating on the surface of another liquid 'B' as shown in the figure, then volume of the liquid displaced by the container
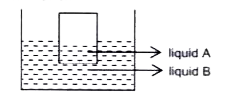    ocr_image

    Ais equal to the weight of the liquid A.
    Bis greater than the weight of the liquid A.
    Cis less than the weight of the liquid A
    DCannot be determined