A coherent beam light of intensity I and absolute wavelength λ=5000Å is being incident on the slits making an angle 30∘ with horizontal. If screen is placed at a distance D=1 m from the slits and the separation between- the slits is 3×10−4m. A thin film of glass μg= 3/2 and thickness 0.41 mm is placed near one slit as shown in the figure, find
(a) the position of central maxima.
(b) the intensity at'point O.
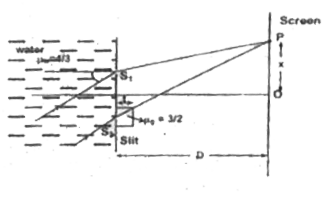
Let central amxima lies at a point P at a distance x from the central line. Then optical path diffenrece Δp at a point P is:
(S2P−t)+tμg−μwdsinθ−S1p
⇒S2P−S1P+(μg−1)t−μwdsinθ
⇒xdD+(μg−1)t−μwdsinθ
For central maxima Δp=0
x=Dd[(μwdsinθ)−(μg−1)t]
13×10−4[43×3×10−4×12−0.5×0.41×10−3]
=5×10−63×10−4=−1.66×10−2m=−1.66m
So central maxima lies at a distance 1.66 cm below the central line
(b) At pointO , optical path difference is
(μg−1)t−μwdsinθ=−5×10−6m
So intensity at 0,
I0=I+I+2√IIcos2π5×10−7(−5×10−6)=4I
Related Playlists
- BOOK - FIITJEECHAPTER - OPTICSEXERCISE - Solved problem (objective)15videos
OPTICS
- BOOK - FIITJEECHAPTER - OPTICSEXERCISE - Comprehension-1(prob)3videos
OPTICS
- BOOK - FIITJEECHAPTER - OPTICSEXERCISE - Illustration10videos
OPTICS
- BOOK - FIITJEECHAPTER - MODERN PHYSICSEXERCISE - Numerical based questions5videos
MODERN PHYSICS
- BOOK - FIITJEECHAPTER - PHYSICS PART-IIIEXERCISE - NUMERICAL BASED QUESTIONS DECIMAL TYPE11videos
PHYSICS PART-III
Similar Practice Problems
- Question 1 - Select One
Light d of wavelength 5000Å is incident normally on a slite. The first minimum of the distance of 5 mm from the central maximum on a screen placed at a distance of 2 m from the slit. The width of slit is
A0.1mmB0.2mmC0.3mmD0.4mm - Question 1 - Select One
Light of wavelength 5000×10−10m is incident normally pattern is observed to lie at distance of 5 mm from the central maximum on screen place at a distance of 3 from the slit. Then the width of the slits is
A3 cmB0.3cmC0.03cmD0.01cm - Question 1 - Select One
Light of wavelength 5000Å is incident normally on a slit. The first minimumof the diffraction pattern is formed at adistance of 5 mm from centra maximum. The screen is situated at a distance of 2 m from the slit. The slit width is
A0.2mmB0.8 mmC0.4mmD2.0mm - Question 1 - Select One
In the Young's double slit experiment, the spacing between two slits is 0.1mm. If the screen is kept at a distance of 1.0m from the slits and the wavelength of ligth is 5000Å, then the fringe width is
A1.0cmB1.5cmC0.5cmD2.0cm - Question 1 - Select One
Light of wavelength 5000 Å is incident on a double with and the interference fringes are formed on a screen plated at a distance of 1m from the slits. If the distance between the two consecutive dark bands is 1 mm, then the distance between the two slits is
A0.5 mmB0.05 mmC1 mmD2 mm - Question 1 - Select One
A light of wavelength 6000Å is incident on a single slit . First minimum is obtained at a distance of 0.4 cm from the centre . If width of the slit is 0.3 mm, the distance between slit and screen will be
A1.0 mB1.5 mC2.0 mD2.3 m - Question 1 - Select One
A monochromatic light of λ=5000Å is inciden on two slits seperated by a distance of 5×10−4m. if a thin glass of thickness 1.5×10−6 m and refractive index 1.5 placed between one of the slits and screen. The pahses difference introduced at the position of central maxima is
A3πB2πC2π/3Dπ/3 - Question 1 - Select One
In the Young's double slit experiment, the spacing between two slits is 0.1mm. If the screen is kept at a distance of 1.0m from the slits and the wavelength of ligth is 5000Å, then the fringe width is
A(a) 1.0cmB(b) 1.5cmC(c) 0.5cmD(d) 2.0cm
Similar Questions
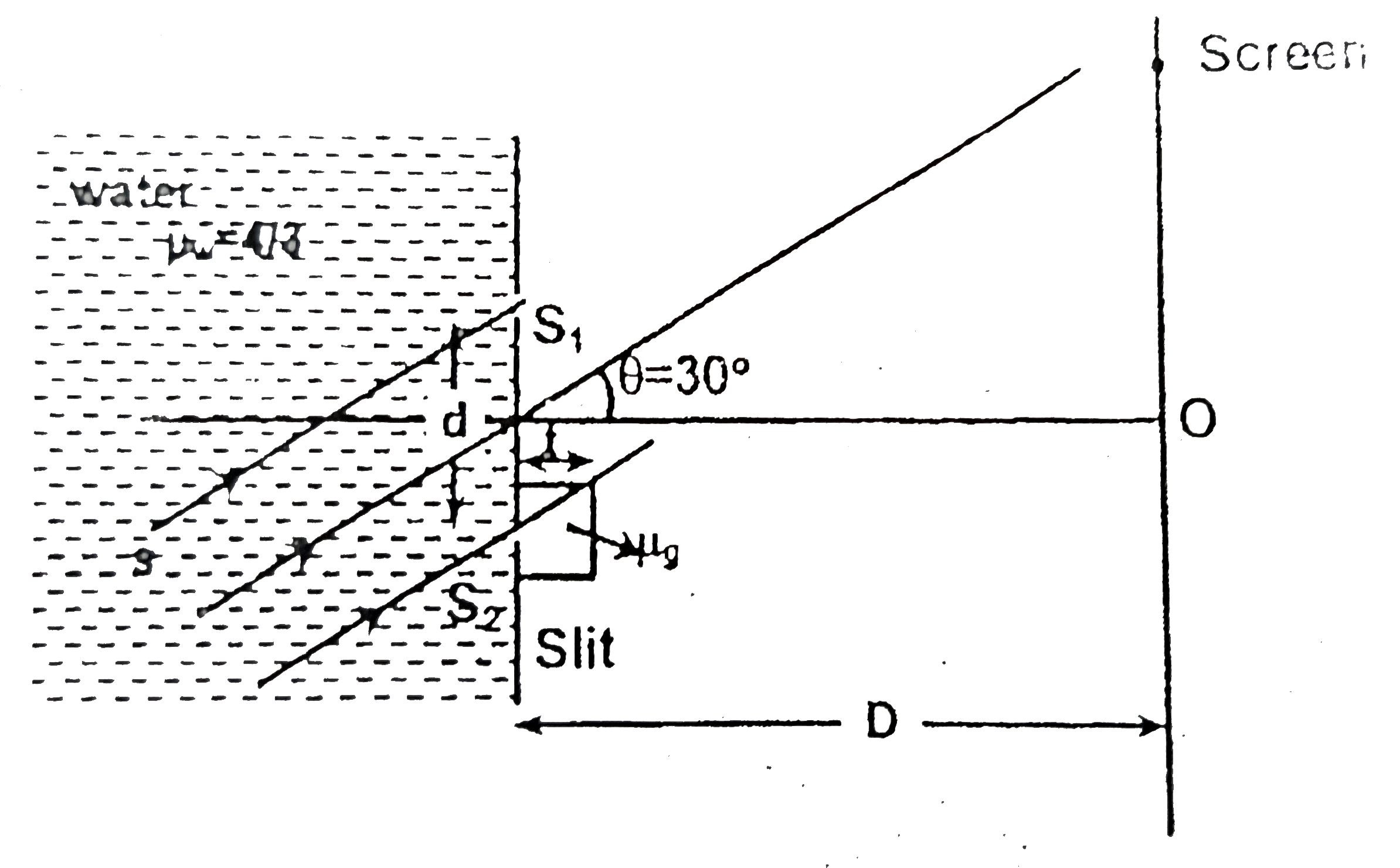
In a YDSE experiment the two slits are covered with a transparent membrane of negligible thickness which allows light to pass through it but does not allow water. A glass slab of thickness t=0.41mm and refractive index μg=1.5 is placed infront of one of the slits as shown in the figure. The separation between the slits is d=0.30mm. The entire space to the left of the slits is filled with water of refractive index μw=4/3.
A coherent light of intensity I and absolute wavelength λ=5000Å is being incident on the slits making an angle 30∘ with horizontal. If screen is placed at a distance D=1m from the slits, find
(a) the position of central maxima.
(b) the intensity at point O.
 View Solution
View SolutionLight of wavelength 5000 Å is incident on a slit of width 0.1 mm. Find out the width of the central bright line on a screen distance 2m from the slit?
View Solution

