Two parallel beams of light P and Q (separation d) containing radiation of wavelengths 4000A and 5000A (which are mutually coherent in each wavelength separately) are incident normally on a prism as shown in fig. The refractive index of the prism as a function of wavelength is given by the relation. μ(λ)=1.20+bλ2 Where λ is in A and b is positive constant. The value of b is such that the condition wave length and is not satisfied for the other.
(a) Find the value of b.
(b) find the deviation of the beams transmitted through the face AC. (c) A convergent lens is used to bring these transmitted beams into focus. If the intensities of transmission form the face AC, are 41 and I respectively, find the resultant intensity at the focus.

Similarly δ2=r2−i2 where i2=θ & r2 can be given as
sini2sinr2=1n2
Putting n2=1.2+b(5000)2=1.2+0.8×106(5000)2
=1.232 and sinθ=0.8
We obtain r2=80∘16.
⇒δ2=80∘16.−sin−10.8≅27∘
Topper's Solved these Questions
- OPTICSBook:FIITJEEChapter:OPTICSExercise:Solved problem (objective)
Explore 15 Videos
- OPTICSBook:FIITJEEChapter:OPTICSExercise:Comprehension-1(prob)
Explore 3 Videos
- OPTICSBook:FIITJEEChapter:OPTICSExercise:Illustration
Explore 10 Videos
- MODERN PHYSICSBook:FIITJEEChapter:MODERN PHYSICSExercise:Numerical based questions
Explore 5 Videos
- PHYSICS PART-IIIBook:FIITJEEChapter:PHYSICS PART-IIIExercise:NUMERICAL BASED QUESTIONS DECIMAL TYPE
Explore 11 Videos
Similar Questions
A biconvex lens of radii of curvature 20 cm has refractive index 1.56 for blue colour and 1.48 for red colour. The approximate linear spread of focus for white light is
View SolutionA ray of light enters a spherical drop of water of refractive index μ as shown in figure.
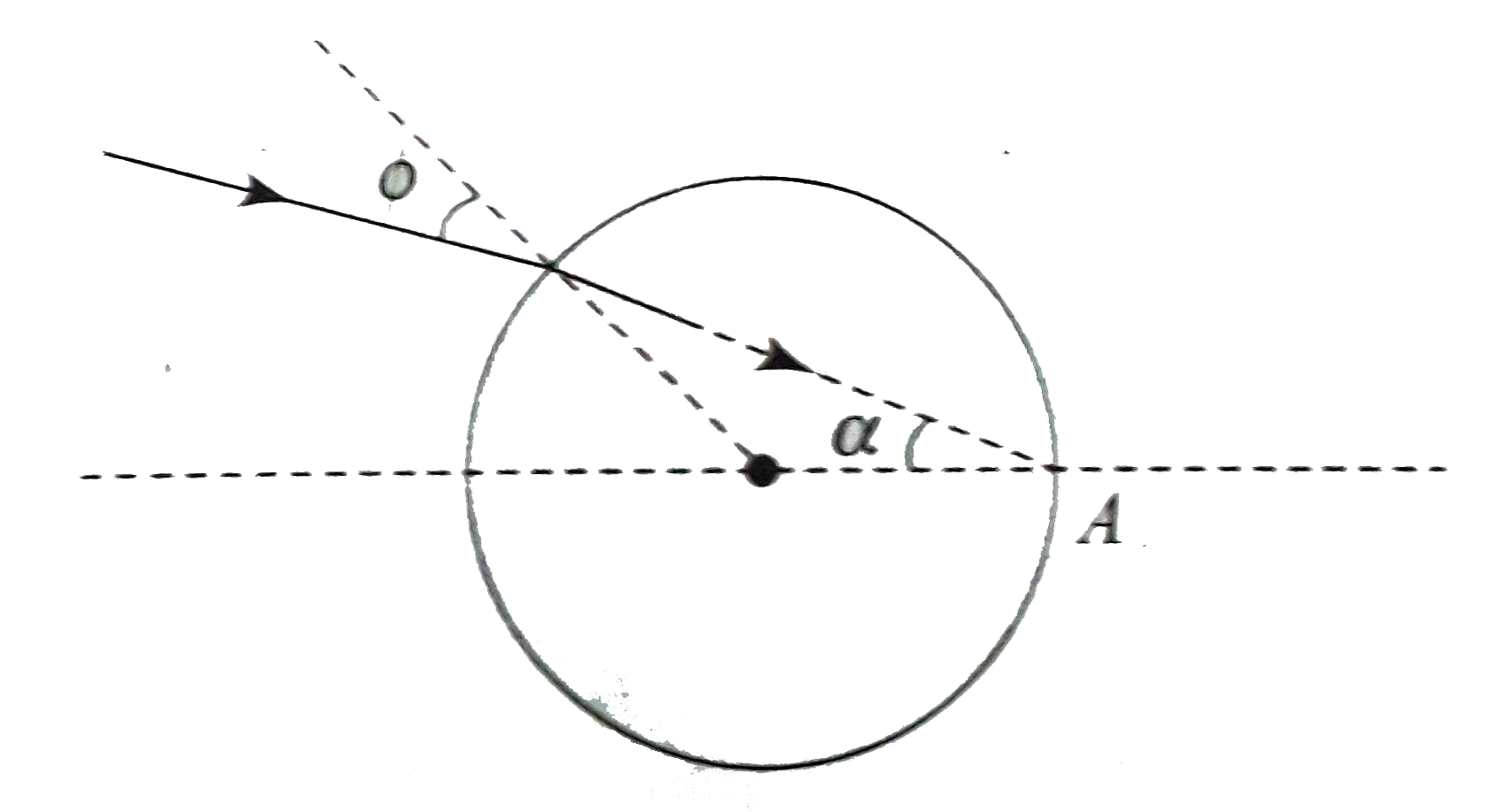
Q. Select the correct statement:
View Solution
If an object moves towards a plane mirror with a speed v at an angle θ to the perpendicular to the plane of the mirror, find the relative velocity between the object and the image.
View SolutionPhotons with energy 5eV are incident on a cathode C in a photoelectric cell . The maximum energy of emitted photoelectrons is 2eV. When photons of energy 6eV are incident on C , no photoelectrons will reach the anode A , if the stopping potential of A relative to C is
View SolutionThe range for a projectile that lands at the same elevation from which it is fired is given by R=(u2/g)sin2θ . Assume that the angle of projection = 30∘. If the initial speed of projection is increased by 1% , while the angle of projection is decreased by 2% . Then by what percentage does the range change ?
View SolutionTwo parallel beams of light P and Q (separation d) containing radiation of wavelengths 4000A and 5000A (which are mutually coherent in each wavelength separately) are incident normally on a prism as shown in fig. The refractive index of the prism as a function of wavelength is given by the relation. μ(λ)=1.20+bλ2 Where λ is in A and b is positive constant. The value of b is such that the condition wave length and is not satisfied for the other.
(a) Find the value of b.
(b) find the deviation of the beams transmitted through the face AC. (c) A convergent lens is used to bring these transmitted beams into focus. If the intensities of transmission form the face AC, are 41 and I respectively, find the resultant intensity at the focus.

View SolutionA beam of light of wavelength 400 nm is incident normally on a right angled prism as shown in Fig. It is observed that light just grazes along the surface AC after falling on it. If refractive index mu of the material of prism varies with wavelength lamda as mu = 1.2 + (b)/(lamda^2) Calculate the value of b and mu of prism material for lamda = 500 nm . Given theta = sin^-1 (0.625) . .
View SolutionAccording to Cauchy's formula, the refractive index mu of a material is related to wavelength lamda as………. .
View SolutionTwo parallel beams of light P and Q (separation d) containing radiations of wavelengts 4000Å and 5000 Å (which are mutually coherent in each wavelength separately) are incident normally on a prism as shown in figure the refractive index of the prism as a function of wavelength is given by the relation mu(lamda)=1.20+(b)/(lamda^(2)) where lamda is in Å and b is a positive constant. The value of b is such that the condition for total reflection at the face AC is just satisfied for one wavelength and is not satisfied for the other. A convergent lens is used to bring these transmitted beams into focus. If the intensities of the upper and the lower beams immediately after transmission from the face AC, are 4I and I respectively, find the resultant intensity at the focus.
View SolutionThe angles of incidence and refraction of a monochromatic ray of light of wavelength λ at an air-glass interface are i and r, respectively. A parallel beam of light with a small spread δλ in wavelength about a mean wavelength λ is refracted at the same air-glass interface. The refractive index μ of glass depends on the wavelength λ as μ(λ)=a+b/λ2 where a and b are constants. Then the angular spread in the angle of refraction of the beam is
View SolutionIf energy of photon is Eproph^(a)c^(b)lamda^(d) . Here h= Planck's constant c= speed of light and lamda= wavelength of photon Then, the value of a,b and d are
View SolutionThe phase difference between oscillatory motion of two points separated by a distance of λ2 is ( where λ is the wavelength)
View SolutionWavelengths of different radiations are given below : lamda (A) = 300nm, lamda (B) = 300mu m, lamda(C) = 3nm, lamda(D) = 30 Å Arrange these radiations in the increasing order of their energies.
View SolutionWhen incident wavelength is λ, stopping potential is 3V0. If incident wavelength is 2λ then stopping potential is V0. Find out threshold wavelength in terms of λ.
View Solution400nm तरंगदैर्ध्य का प्रकाश पुंज एक समकोणिक प्रिज्म पर लंबवत आपतित होता है। यह देखा जाता है कि प्रकाश पुंज पृष्ठ AC पर पढ़कर इससे स्पर्श रेखीय निकलता है (नीचे दिए गया चित्र। प्रिज्म के पदार्थ का अपवर्तनांक तरंगदैर्य (λ) के साथ निम्न प्रकार बदलता है
μ=1.2+bλ2
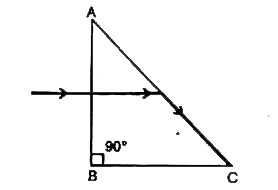
b का मान तथा λ=500nm के लिए प्रिज्म के पदार्थ का अपवर्तनांक ज्ञात कीजिय। दिया है θ=sin−1(0.625)
View SolutionThe refractive index ( mu ) of glass is related to the wavelength (lambda) of incident light as mu = A +(B)/(lambda^(2)) , where A and B are constants. Find out the dimensions of A and B.
View Solution