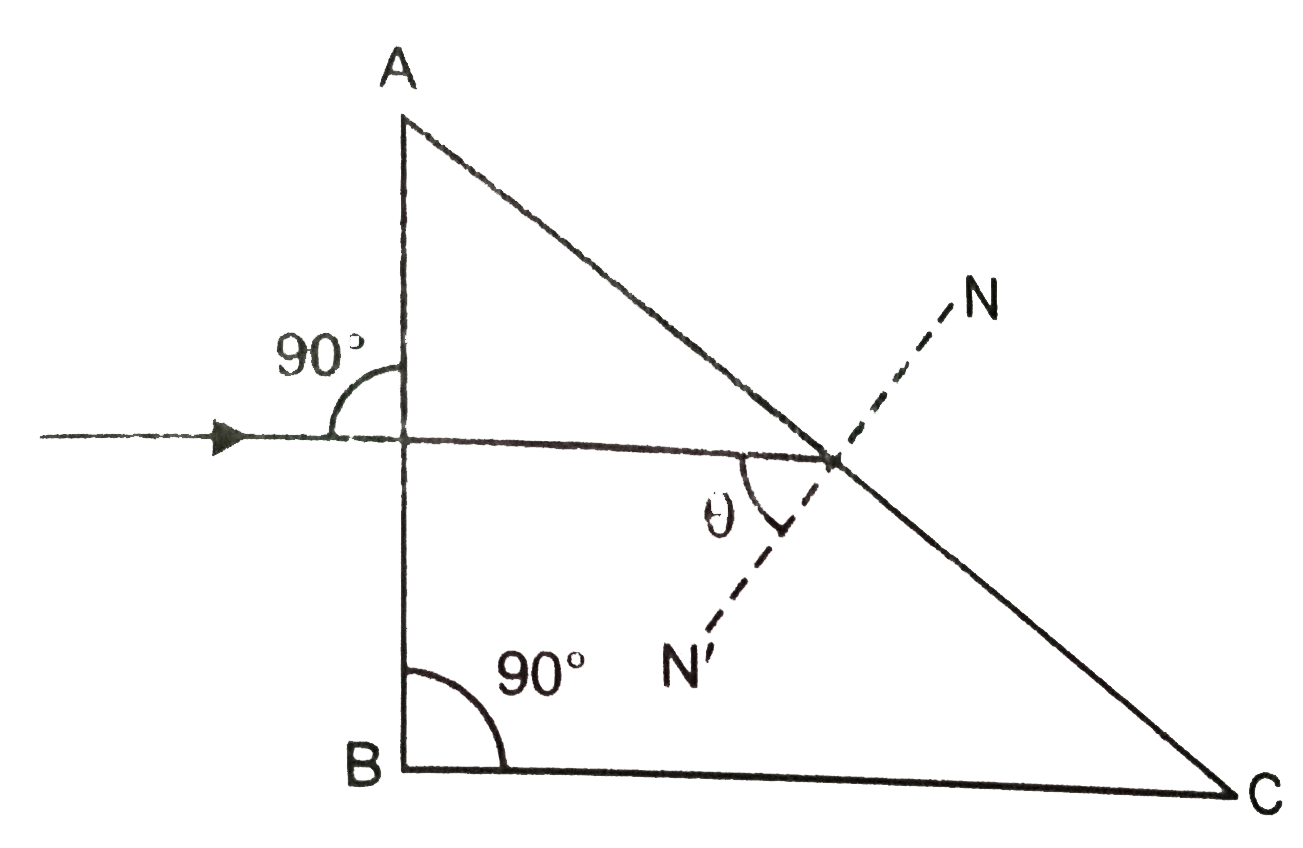
A beam of light of wavelength 400nm is incident normally on a right angled prism as shown in Fig.
It is observed that light just grazes along the surface AC after falling on it. If refractive index μ of the material of prism varies with wavelength
λ as μ=1.2+bλ2
Calculate the value of bandμ of prism material for λ=500nm. Given θ=sin−1(0.625).
 .
.
As the ray goes grazingly along AC,θ must be the critical angle.
From μ=1sinC=1sinθ=10.625=1.6
As μ=1.2+bλ2
1.6=1.2+b(400)2
b=0.4×(400)2=64000nm2
For λ=500nm, the refractive index of the material of the prism is
μ=1.2+bλ2=1.2+64000(500)2=1.2+0.256
μ=1.456.
Topper's Solved these Questions
- RAY OPTICSBook:PRADEEPChapter:RAY OPTICSExercise:Solved Example(c )
Explore 21 Videos
- RAY OPTICSBook:PRADEEPChapter:RAY OPTICSExercise:Solved Example(d)
Explore 32 Videos
- RAY OPTICSBook:PRADEEPChapter:RAY OPTICSExercise:Sample problem(d)
Explore 5 Videos
- PROPERTIES OF BULK MATTERBook:PRADEEPChapter:PROPERTIES OF BULK MATTERExercise:Multiple choice questions
Explore 7 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:PRADEEPChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:Assertion- Reason Type questions
Explore 20 Videos
Similar Questions
A ray of light is incident horizontally on the face AB of the.right angled prism as shown in the figure. If the ray emerges grazing the surface AC, find the value of ϕ. Refractive index of the material of the prism is given to be n.
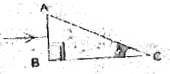
View SolutionAccording to Cauchy's formula, the refractive index μ of a material is related to wavelength λ as………. .
View Solution
Knowledge Check
When light of wavelength λ on an equilateral prism, kept on its minimum deviation position, it is found that the angle of deviation equals the angle the angle of the prism itself. The refractive index of the material of the prism for the wavelength λ is
A√32B√3C2D√2When light of wavelength λ on an equilateral prism, kept on its minimum deviation position, it is found that the angle of deviation equals the angle the angle of the prism itself. The refractive index of the material of the prism for the wavelength λ is
A√3B√3/2C2D√2A monochromatic ray of light is incident normally on one of the refracting surfaces of a prism . The emergent ray grazes the second refracting surface . What is the angle of the prism if the refractive index of the material of the prism is 1.6 ?
AA<2CBA = 2CCA>2CDA<C2
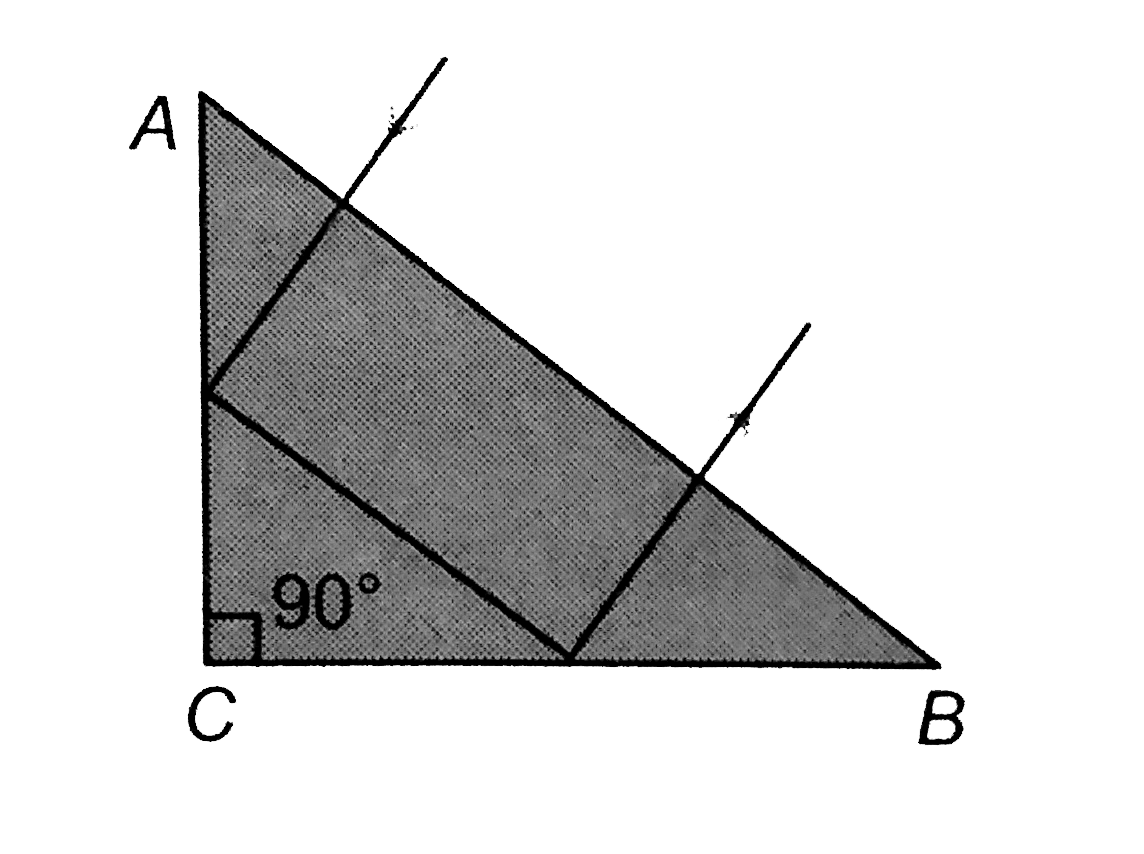
A ray of light incident normally on an isosceles right angled prism travels as shown in the figure. The least value of the refractive index of the prism must be
View SolutionA monochromatic ray of light is incident normally on one of the refracting surfaces of a prism . The emergent ray grazes the second refracting surface . What is the angle of the prism if the refractive index of the material of the prism is 1.6 ?
View SolutionWhen a ray of light is incident normally on one refracting surface of an equilateral prism (Refractive index of the material of the prism =1.5
View SolutionA ray of light is incident normally on one of the refracting surfaces of a prism of refracting angle A,. The emergent ray grazes the other refracting surface. Find the refractive index of the material ofprism.
View SolutionA monochromatic ray of light is incident normally on one of the refracting surfaces of a prism . The emergent ray grazes the second refracting surface . What is the angle of the prism if the refractive index of the material of the prism is 1.6 ?
View Solution

