Assertion : In rolling, all points of a rigid body have the same linear velocity.
Reason : The rotational motion does not affect the linear velocity.
If both, Assertion and Reason are true and the Reason is the correct explanation of the Assertion.
If both, Assertion and Reason are true but Reason is not a correct explanation of the Assertion.
If Assertion is true but the Reason is false.
If both, Assertion and Reason are false.
The correct Answer is:D
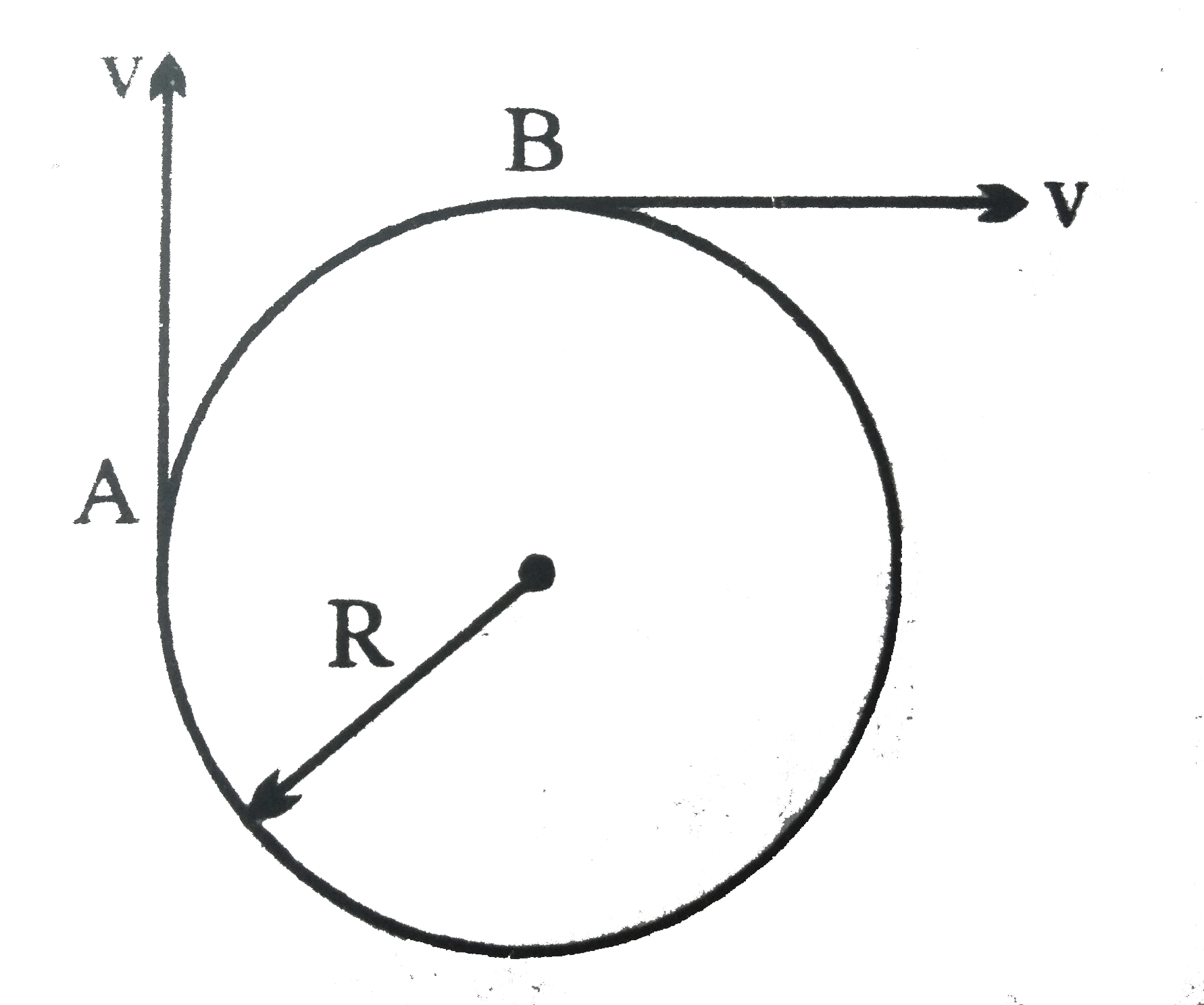
Here, both the assertion and reason are false because in case of a rolling body, all points on it have same angualr but different linear speed. Linear speed is different at different places. It is max. at highest point and minimum at lowest point.
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:PRADEEPChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:Integer Type Questions
Explore 13 Videos
- RAY OPTICSBook:PRADEEPChapter:RAY OPTICSExercise:Problem For Practice(a)
Explore 25 Videos
- THERMODYNAMICSBook:PRADEEPChapter:THERMODYNAMICSExercise:Assertion- Reason Type Questions
Explore 19 Videos
Similar Questions
Knowledge Check
A : In pure rolling motion all the points of a rigid body have same linear velocity.
R : Rolling motion is not possible on smooth surface.AIf both Assertion & Reason are true and the reason is the correct explanation of the assertion,BIf both Assertion & Reason are true but the reason is not the correct explanation of the assertion,CIf Assertion is true statement but Reason is false,DIf both Assertion and Reason are false statements,In rotational motion of a rigid body, all particles move with
ASame linear and angular velocityBSame linear and different angular velocityCWith different linear velocities and same angular velocitiesDWith different linear velocities and different angular velocitiesIn rotational motion of a rigid body, all particles move with
Asame linear and angular velocity.Bsame linear velocity and different angular velocities.Cdifferent limear velocities and same angular velocity.Ddifferent linear and angular velocities.
Consider the following two statements A and B and identify the correct choice
A) When a rigid body is rotating about its own axis, at a given instant all particles of body posses same angular velocity.
B) When a rigid body is rotating about its own axis, the linear velocity of a particle is directly proportional to its perpendicular distance from axis
View SolutionAssertion : The angular velocity of a rigid body in motion is defined for the whole body
Reason : All points on a rigid body performing pure rotational motion are having same angular velocity.
View SolutionA thin ring and a solid disc of same mass and radius are rolling with the same linear velocity. Then ratio of their kinetic energies is
View SolutionAssertion: A body having non zero acceleration can have a constant velocity.
Reason: Acceleration is the rate of change of velocity.
View SolutionThe linear velocity of a point on the surface of earth at a latitude of 60∘ is
View Solution


 .
.