Statement -1 : In the formation of a neutron star, spin angular velocity increases tremendously.
Statement-2 : Conservation of rotational kinetic energy
Statement-1 is true, Statement-2 is true ,
Statement-2 is correct explanation of Statement-1.
Statement-1 is true, Statement-2 is true but Statement-2 is not correct explanation of Statement-1.
Statement-1 is true, but statement-2 is false.
Statement-1 is false, but statement-2 is true.
The correct Answer is:C
Statement-1 is true, but the statement-2 is false. Inface, in the formation of a neutron star, a heavy contraction occurs on account of termendous gravitational pull. Moment of inertia Idecreases. As L=Iω= constant, therefore, ω increases i.e. spin angular velocity increases.
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:PRADEEPChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:Integer Type Questions
Explore 13 Videos
- RAY OPTICSBook:PRADEEPChapter:RAY OPTICSExercise:Problem For Practice(a)
Explore 25 Videos
- THERMODYNAMICSBook:PRADEEPChapter:THERMODYNAMICSExercise:Assertion- Reason Type Questions
Explore 19 Videos
Similar Questions
Knowledge Check
If the angular velocity of a body increases by 20% then its kinetic energy of rotation will increase by
A20%B30%C44%D66%K the angular velocity of a body increases by 40%, its kinetic energy of rotation increases by
A80%B20%C96%DNone of theseA ballet dancer is rotating about his own vertical axis. Without external torque if his angular velocity is doubled then his rotational kinetic energy is
AhalvedBdoubledCquadrupledDunchanged
A rod of mass m and length l is connected with a light rod of length l. The composite rod is made to rotate with angular velocity ω as shown in the figure. Find the
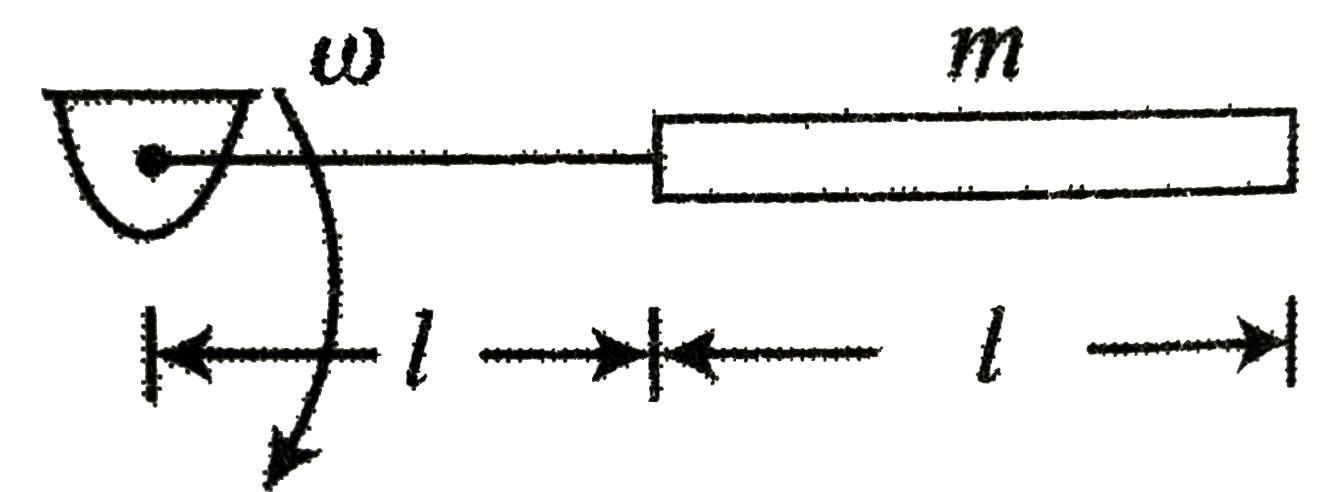
a. translational kinetic energy.
b. rotational kinetic energy.
c. total kinetic energy of rod.
View SolutionQuestions on Rotational Kinetic Energy and Angular Momentum
View SolutionConsider a one dimensional head on collision of two balls.
Statement-1 : The loss in kinetic energy of the system during the collision does not depend on the velocity of the observer.
Statement-2 : Kinetic energy of a body is independent of velocity of observer.
View Solution
Two identical discs are positioned on a vertical axis as shown in the figure. The bottom disc is rotating at angular velocity ω0 and has rotational kinetic energy K0. Change in the rotational kinetic energy of the system is
View SolutionIf angular momentum is conserved in a system whose moment of inertia is decreased, will rotational kinetic energy be conserved.
View Solution