In the YDSE, the monochromatic source of wavelength λ is placed at a distance d2 from the central axis (as shown in the figure), where d is the separation between the two slits S1andS2 .
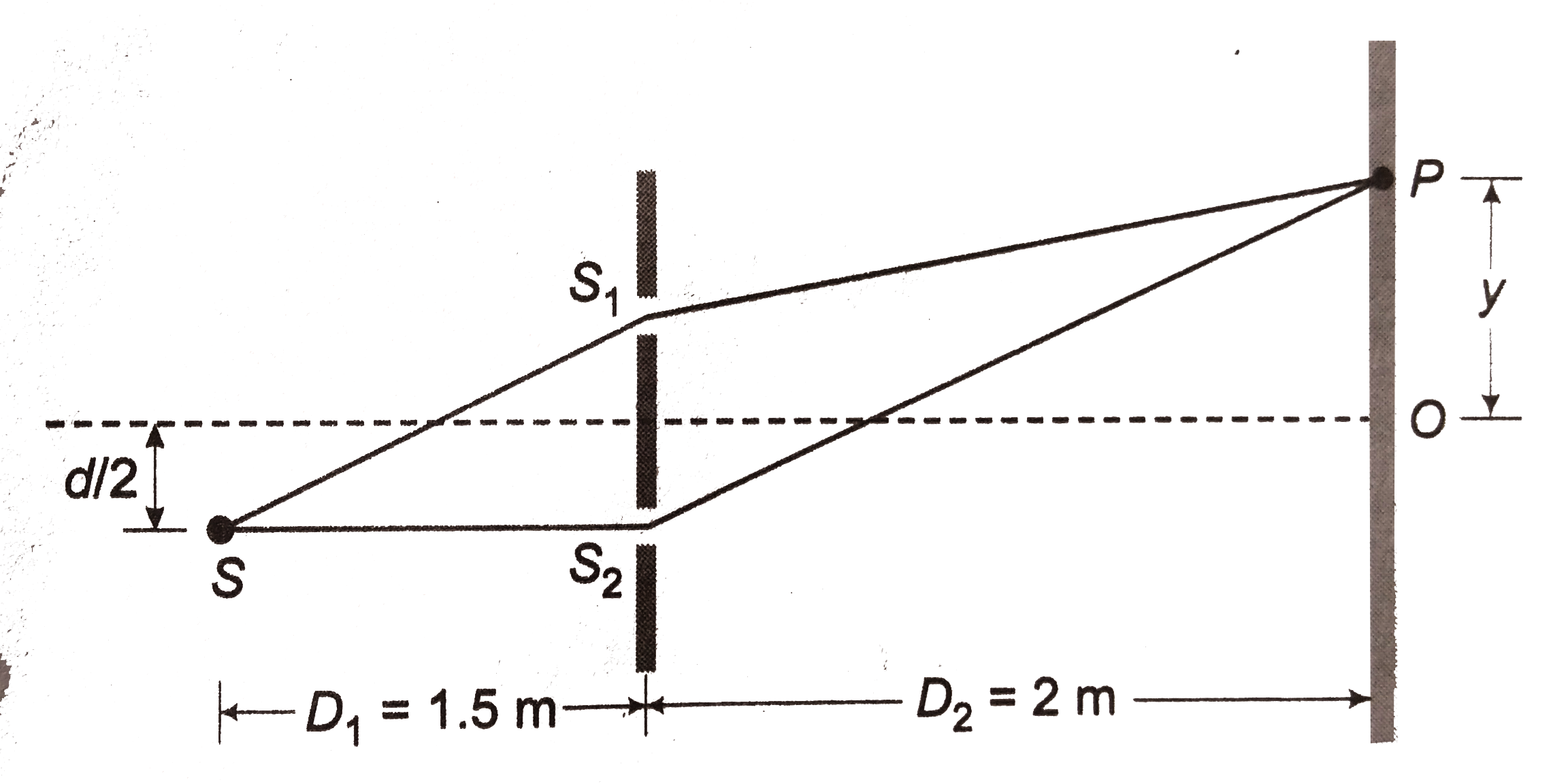
(a)Find the position of the central maxima.
(b) Find the order of interference formed at O.
(c)Now, S is placed on centre dotted line. Find the minimum thickness of the film of refractive indes μ=1.5 to be placed in front of S2 so that intensity at O becomes 34th of the maximum intensity.
(Take λ=6000Å,d=6mm.)
(a) (Δx)net=0
∴y1dD1=y2dD2
∴d/21.5=y2.0
or y=d1.5
=61.5
=4mm.
(b) At O, net path difference,
Δx=y1dD1
=(d/2)dD1
=(6×10−3)2)2×1.5
=12×10−6m
=120×10−7m
λ=6000Å
=6×10−7m
As, Δx=20λ, therefore at O bright fringe of
order 20 will be obtained.
(c)I=Imaxcos2ϕ2
34Imax=Imaxcos2ϕ2
∴ϕ2=π6
ϕ=π3=2πλ(μ−1)t
∴t=λ6(μ−1)
60006(1.5−1)
=2000Å.
Topper's Solved these Questions
- INTERFERENCE AND DIFFRACTION OF LIGHTBOOK - DC PANDEYCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Level 2 Comprehensionn Based
4 Videos
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - All Questions
120 Videos
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEYCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery
59 Videos
Similar Questions
A young's double slit apparatus is immersed in a liquid of refractive index 1.33.It has slit separation of 1 mm and interference pattern is observed on the screen at a distance 1.33 m from plane of slits. The wavelength in air is 6300Å
Calculate the fringe width.
View SolutionAn infinite number of particles each of mass m are placed on the positive X-axis of 1m,2m,4m,8m,... from the origin. Find the magnitude of the resultant gravitational force on mass m kept at the origin.
View SolutionA long wire carries a steady curent . It is bent into a circle of one turn and the magnetic field at the centre of the coil is B. It is then bent into a circular loop of n turns. The magnetic field at the centre of the coil will be
View SolutionConsider the situation shown in figure. The two slits S1andS2 placed symmetrically around the central line are illuminated by a monochromatic light of wavelength λ. The separation between the slits is d. The light transmitted by the slits falls on a screen Σ1 placed at a distance D from the slits. The slit S3 is at the placed central line and the slit S4, is at a distance z from S3. Another screenΣ2 is placed a further distance D away from 1,1. Find the ratio of the maximum to minimum intensity observed on Σ2 if z is equal to a. z=λD2d b. λDd c. λD4d

View SolutionConsider the situation shown in fig. The two slits S_(1) and S_(2) placed symmetrically around the central line are illuminated by monochromatic light of wavelength lambda . The separation between the slit is d. The ligth transmitted by the slits falls on a screen S_(0) placed at a distance D form the slits. The slit S_(3) is at the central line and the slit S_(4) is at a distance z from S_(3) Another screen S_(c) is placed a further distance D away from S_(c) Find the ratio of the maximum to minimum intensity observed on S_(c) If z = (lambda D)/(2 d)
View SolutionConsider the situation shown in fig. The two slits S1 and S2 placed symmetrically around the central line are illuminated by monochromatic light of wavelength λ. The separation between the slit is d. The ligth transmitted by the slits falls on a screen S0 placed at a distance D form the slits. The slit S3 is at the central line and the slit S4 is at a distance z from S3 Another screen Sc is placed a further distance D away from Sc Find the ratio of the maximum to minimum intensity observed on Sc
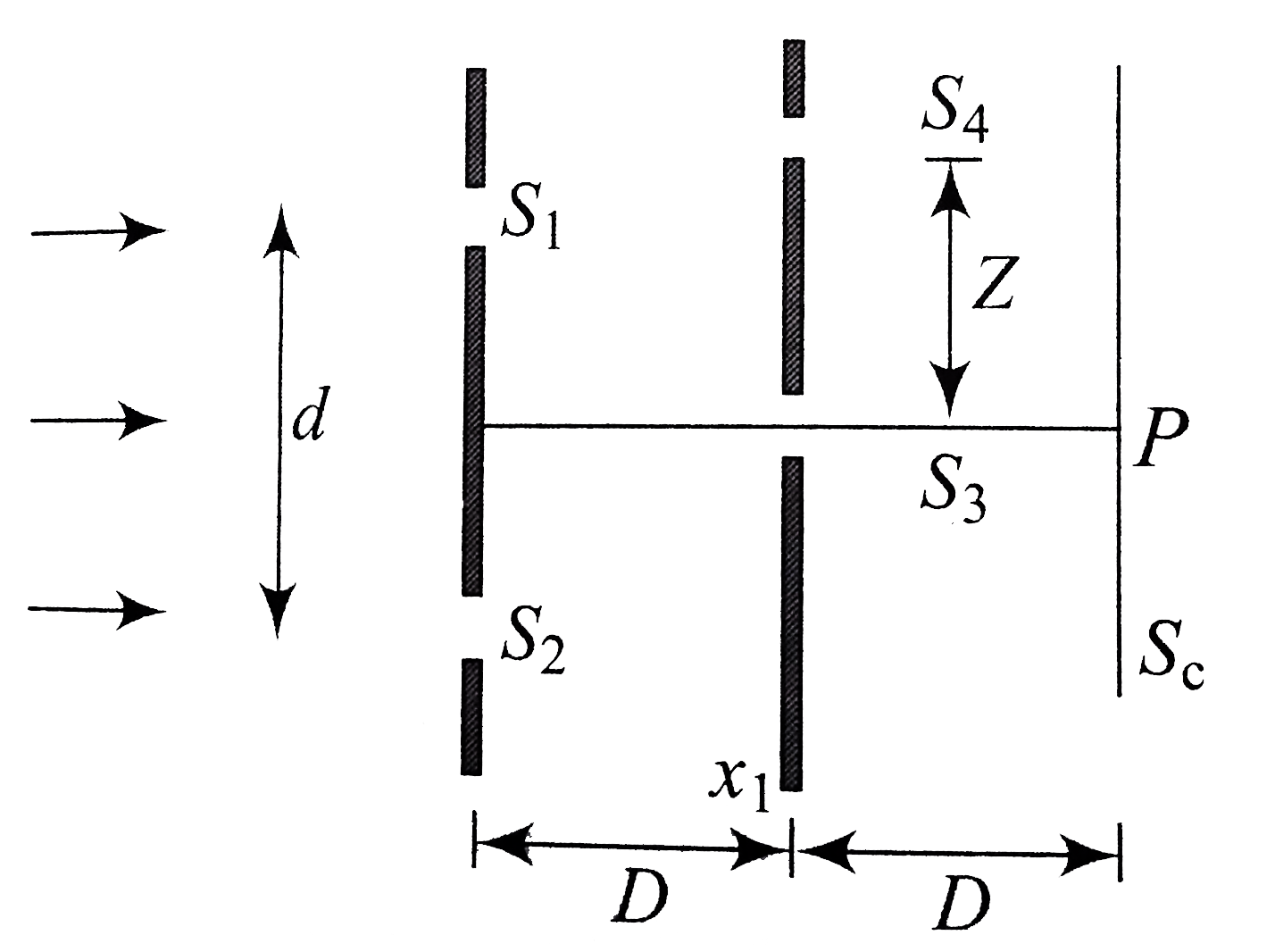
If z=λD4d
View SolutionIn YDSE arrangement as shown in figure, fringes are seen on screen using monochromatic source S having wavelength 3000 Å (in air). S_1 and S_2 are two slits seperated by d = 1 mm and D = 1m. Left of slits S_1 and S_2 medium of refractive index n_1 = 2 is present and to the right of S_1 and S_2 medium of n_2 = 3/2 , is present. A thin slab of thickness 't' is placed in front of S_1 . The refractive index of n_3 of the slab varies with distance from it's starting face as shown in figure. In order to get central maxima at the centre of screen, the thickness of slab required is :
View SolutionThe two coherent sources of monochromatic light of wavelength lambda are located at a separation lambda . The two sources are placed on a horizontal line and screen is placed perpendicular to the line joining the sources. Find position of the farthest minima from the centre of the sources.
View SolutionIn YDSE a = 2mm , D = 2m, lambda = 500 mm. Find distance of point on screen from central maxima where intensity becomes 50% of central maxima
View SolutionIn a YDSE, D = 1m, d = 1mm and lambda = 1//2 mm Find a distance between the first and central maxima on the screen.
View SolutionIn the YDSE the monochromatic source of wavelength λ is placed at a distance d2 from the central axis (as shown in the figure), where d is the separation between two slits S1 and S2. Find the position of the central maxima. (Given d = 6 mm)
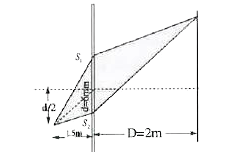
View SolutionIn a Young's double slit interference experiment the fringe pattern is observed on a screen placed at a distance D from the slits. The slits are separated by a distance d and are illuminated by monochromatic light of wavelength λ. Find the distance from the central point where the intensity falls to (a) half the maximum, (b) one fourth of the maximum.
View SolutionConsider the situation shown in figure. The two slits S1andS2 placed symmetrically around the central line are illuminated by a monochromatic light of wavelength λ. The separation between the slits is d. The light transmitted by the slits falls on a screen Σ1 placed at a distance D from the slits. The slit S3 is at the placed central line and the slit S4, is at a distance z from S3. Another screenΣ2 is placed a further distance D away from 1,1. Find the ratio of the maximum to minimum intensity observed on Σ2 if z is equal to a. z=λD2d b. λDd c. λD4d

View SolutionLight of wavelength lambda= 500 nm falls on two narrow slits placed a distance d= 50 xx 10^(-4) cm apart, at an angle phi= 30^@ relative to the slits shown in figure. In front of the lower slit, a slab of thickness 0.1 mm and refractie index 3/2 is placed. THe interference pattern is observed on a screen at a distance D= 2m from the slits S_1 O = S_2 O = d//2 The position of central maxima is at an angular position theta with line OB
View SolutionIn the YDSE the monochronic source of wavelength λ is palced at a distance d2 from the central axis (as shown in the figure ) , where d is the separation between two slits S1andS2 .Find the position of the central maxima . (Given d = 6 mm )
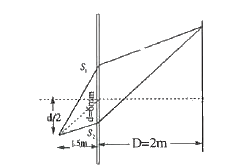
View Solution
