Triangle ABC is such that AB=9cm,BC=6cm,AC=7.5cm. Triangle DEF is similar to ΔABC. If EF = 12 cm then DE is :
6 cm
16 cm
18 cm
15 cm
The correct Answer is:C
To solve the problem, we will use the property of similar triangles, which states that the ratios of corresponding sides of similar triangles are equal.
1. Identify the sides of triangle ABC:
- AB = 9 cm
- BC = 6 cm
- AC = 7.5 cm
2. Identify the corresponding side in triangle DEF:
- EF = 12 cm (given)
3. Set up the proportion using the similarity of triangles:
Since triangle DEF is similar to triangle ABC, we can write the following proportion:
DEAB=EFBC
4. Substitute the known values into the proportion:
- We know AB = 9 cm and BC = 6 cm, and EF = 12 cm. Therefore, we can substitute these values into the proportion:
DE9=126
5. Simplify the right side of the equation:
- The fraction 126 simplifies to 2. Thus, we have:
DE9=2
6. Solve for DE:
- To find DE, multiply both sides of the equation by 9:
DE=2×9=18 cm
Final Answer:
- DE = 18 cm
- AB = 9 cm
- BC = 6 cm
- AC = 7.5 cm
- EF = 12 cm (given)
Since triangle DEF is similar to triangle ABC, we can write the following proportion:
DEAB=EFBC
- We know AB = 9 cm and BC = 6 cm, and EF = 12 cm. Therefore, we can substitute these values into the proportion:
DE9=126
- The fraction 126 simplifies to 2. Thus, we have:
DE9=2
- To find DE, multiply both sides of the equation by 9:
DE=2×9=18 cm
- DE = 18 cm
Topper's Solved these Questions
- GEOMETRYBook:ARIHANT SSCChapter:GEOMETRYExercise:INTRODUCTORY EXERCISE - 12.3
Explore 28 Videos
- GEOMETRYBook:ARIHANT SSCChapter:GEOMETRYExercise:INTRODUCTORY EXERCISE - 12.4
Explore 10 Videos
- GEOMETRYBook:ARIHANT SSCChapter:GEOMETRYExercise:INTRODUCTORY EXERCISE - 12.1
Explore 45 Videos
- FUNDAMENTALS Book:ARIHANT SSCChapter:FUNDAMENTALS Exercise:TEST OF YOU - LEARNING - 2
Explore 40 Videos
- HCF AND LCMBook:ARIHANT SSCChapter:HCF AND LCMExercise:Exercise Higher Skill Level Questions
Explore 18 Videos
Similar Questions
Knowledge Check
Triangle ABC is such that AB=9cm,BC=6cm,AC=7.5cm. Triangle DEF is similar to ΔABC. If EF = 12 cm then DE is :
A6 cmB16 cmC18 cmD15 cmIn Δ PQR, PQ = 4 cm, QR = 3 cm, and RP = 3.5 cm. Δ DEF is similar to Δ PQR. If EF = 9 cm, then what is the perimeter of Δ DEF ?
A10.5 cmB21 cmC31.5 cmDCannot be determined as data is insufficientIn ΔABC, it is given that AB=9cm,BC=6cm,andCA=7.5cm. AlsoΔDEF is givne such that EF=8cmandΔDEF~ΔABC. Then perimeter of ΔDEF is
A22.5cmB25cmC27 cmD30 cm
In △ABC, AB = 6 cm, AC = 8 cm, and BC = 9 cm. The length of median AD is:
View SolutionIf triangle ABC is similar to triangle DEF such that 2AB = DE and BC = 8 cm then EF is .
View SolutionD and E are respectively the points on the sides AB and AC of a triangle ABC such that AD=2cm, BD=3cm,BC=7.5cm and DE || BC. Then length of DE (in cm) is
(a) 2.5
(b) 3
(c) 5
(d) 6
View SolutionIn △ABC,AB=6cm,AC=8cm,andBC=9cm. The length of median AD is :
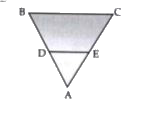
View SolutionIn figure ,DE||BC in triangle ABC such that BC = 8 cm , AB = 6 cm and DA = 1.5 cm .find DE.
View Solution