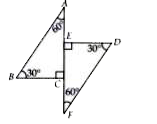
In the adjoining figure D is the midpoint of BC of a ΔABC,DMandDN are the perpendiculars on AB and AC respectively and DM=DN, then the ΔABC is :

right angled
isosceles
equilateral
scalene
The correct Answer is:B
Step by step video, text & image solution for In the adjoining figure D is the midpoint of BC of a DeltaABC, DM and DN are the perpendiculars on AB and AC respectively and DM = DN, then the DeltaABC is : by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Topper's Solved these Questions
- BOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - INTRODUCTORY EXERCISE - 12.328videos
GEOMETRY
- BOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - INTRODUCTORY EXERCISE - 12.410videos
GEOMETRY
- BOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - INTRODUCTORY EXERCISE - 12.145videos
GEOMETRY
- BOOK - ARIHANT SSCCHAPTER - FUNDAMENTALS EXERCISE - TEST OF YOU - LEARNING - 240videos
FUNDAMENTALS
- BOOK - ARIHANT SSCCHAPTER - HCF AND LCMEXERCISE - Exercise Higher Skill Level Questions18videos
HCF AND LCM
Similar Questions
Knowledge Check
- Question 1 - Select One
In a ΔABC,AB=ACandAD⊥BC, then:
AAB<ADBAB>ADCAB=ADDAB≤AD - Question 2 - Select One
In the adjoining figure, ABC is an isosceles triangle in which AB = AC. If E and F be the midpoints of AC and AB respectively, then
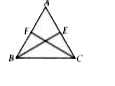 ABE = CFB∠BFC=∠CEBCBF = CEDAll of these
ABE = CFB∠BFC=∠CEBCBF = CEDAll of these - Question 3 - Select One
In the adjoining figure, ABC is an isosceles triangle in which AB=AC. If E and F be the midpoints of AC and AB respectively, then
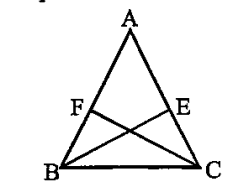 ABE=CFB∠BFC=∠CEBCBF=CEDAll of these
ABE=CFB∠BFC=∠CEBCBF=CEDAll of these
In an adjoining figure, ABCD is a rectangle, BM and DN are perpendicular from B and D on AC (i) Is ΔBMC=ΔDNA
View SolutionIn the adjoining figure D, E and F are the mid - points of the sides BC, AC and AB respectively to triangle. Show that ∠EDF=∠A, ∠DEF=∠B and ∠DFE=∠C:
 View Solution
View SolutionIn Figure, ABCD is a rectangle. BM and DN are perpendicular from B and D respectively on AC . Prove that MBC≅DNA (ii) BM=DN
View SolutionIn the adjoining figure, M is the midpoint of seg AB and seg CM is a median of ΔABC. Find A(ΔAMC)A(ΔBMC).
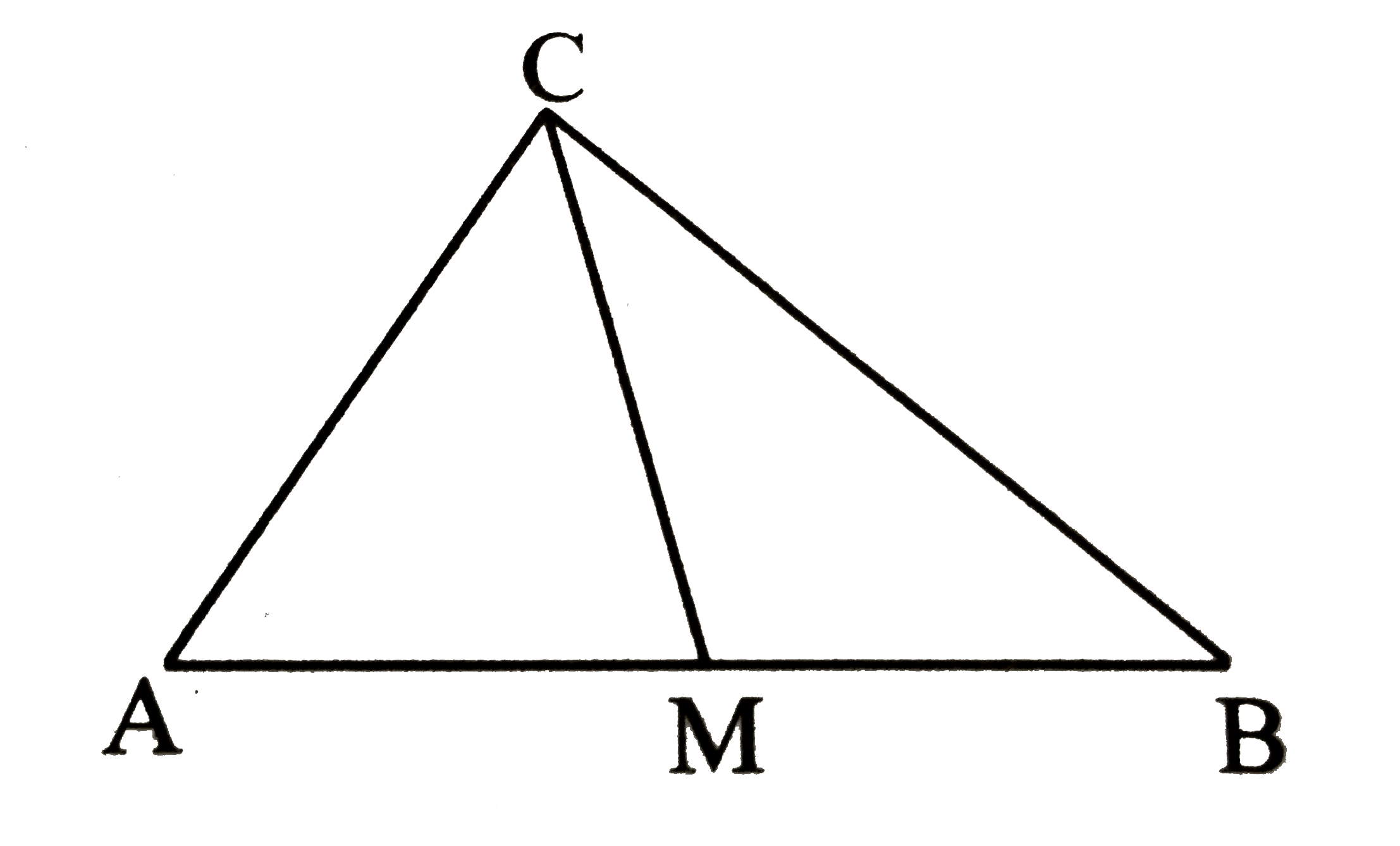 View Solution
View SolutionArea of ΔABC=30cm2. D and E are the mid - points of BC and AB respectively. Find A(ΔBDE) :
View Solution