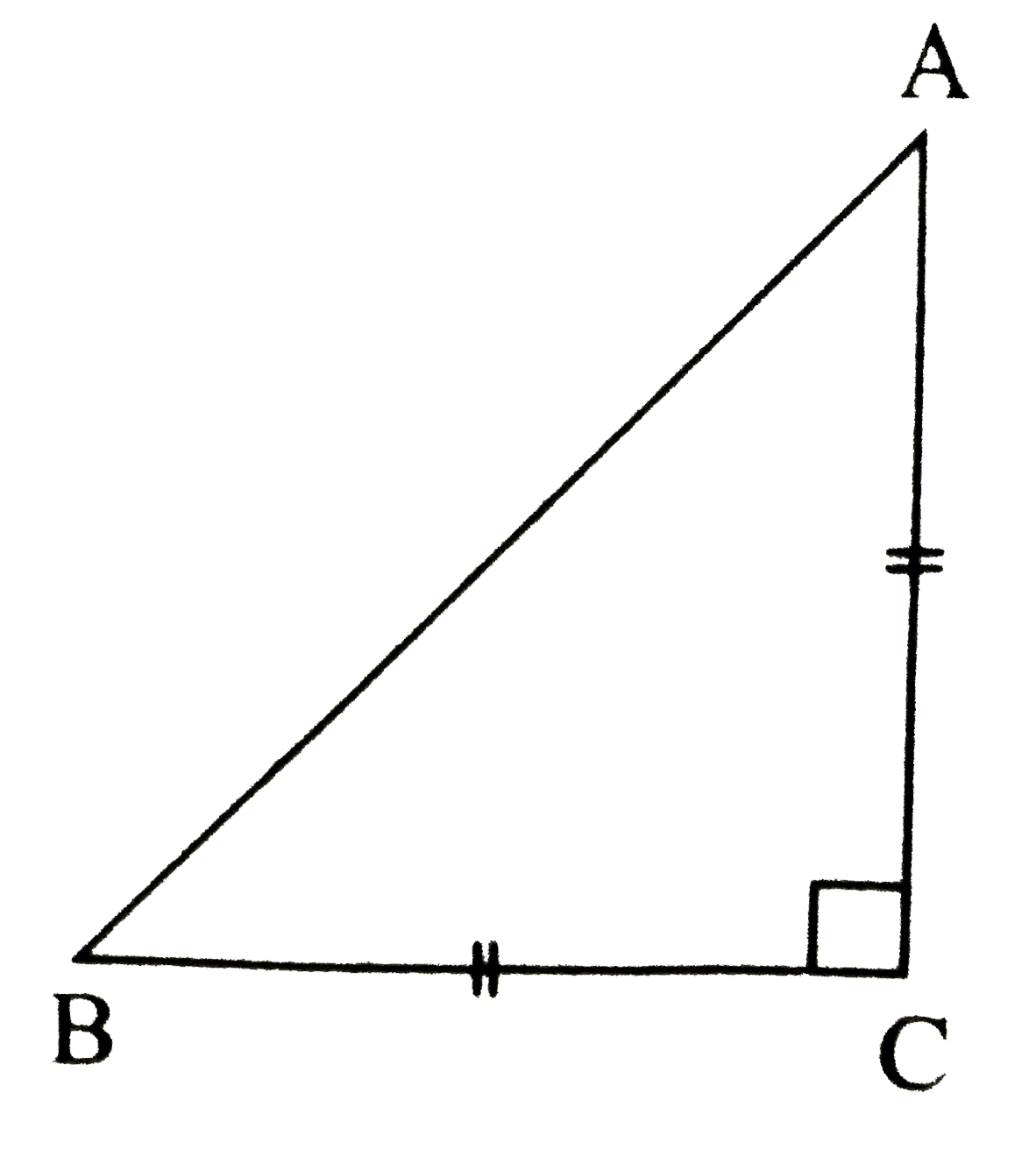
In a ΔABC,AB=ACandAD⊥BC, then:
AB<AD
AB>AD
AB=AD
AB≤AD
The correct Answer is:B
To solve the problem step by step, we will analyze the given information and derive the relationship between the segments in triangle ABC.
1. Identify the Triangle: We have triangle ABC where AB = AC, indicating that it is an isosceles triangle.
Hint: Recall that in an isosceles triangle, the two sides opposite the equal angles are equal.
2. Draw the Perpendicular: A perpendicular line AD is drawn from point A to line BC. This means that AD is the altitude of the triangle from vertex A to side BC.
Hint: Remember that the altitude of a triangle is a line segment from a vertex perpendicular to the opposite side.
3. Properties of Isosceles Triangle: Since triangle ABC is isosceles (AB = AC), the altitude AD also acts as the median to side BC. This means that point D, where AD meets BC, divides BC into two equal segments, BD and DC.
Hint: In an isosceles triangle, the altitude from the vertex to the base bisects the base.
4. Analyze the Right Triangle: In triangle ABD, we have a right triangle where AD is the altitude, AB is one of the equal sides, and BD is half of the base BC.
Hint: Use the Pythagorean theorem to analyze the relationship between the sides of the right triangle.
5. Apply the Pythagorean Theorem: According to the Pythagorean theorem:
AB2=AD2+BD2
Since BD is a positive length, it follows that:
AD2<AB2
Taking the square root of both sides gives:
AD<AB
Hint: The Pythagorean theorem states that in a right triangle, the square of the hypotenuse (AB) is equal to the sum of the squares of the other two sides (AD and BD).
6. Conclusion: Since we have established that AD < AB, we can conclude that AB is greater than AD. Therefore, the correct option is:
- AB > AD
Hint: Compare the lengths of the altitude and the sides of the triangle to determine their relationships.
Final Answer:
AB is greater than AD (Option 2).
AB2=AD2+BD2
Since BD is a positive length, it follows that:
AD2<AB2
Taking the square root of both sides gives:
AD<AB
- AB > AD
AB is greater than AD (Option 2).
Topper's Solved these Questions
- GEOMETRYBOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - INTRODUCTORY EXERCISE - 12.3
28 Videos
- GEOMETRYBOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - INTRODUCTORY EXERCISE - 12.4
10 Videos
- GEOMETRYBOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - INTRODUCTORY EXERCISE - 12.1
45 Videos
- FUNDAMENTALS BOOK - ARIHANT SSCCHAPTER - FUNDAMENTALS EXERCISE - TEST OF YOU - LEARNING - 2
40 Videos
- HCF AND LCMBOOK - ARIHANT SSCCHAPTER - HCF AND LCMEXERCISE - Exercise Higher Skill Level Questions
18 Videos
Similar Questions
Knowledge Check
In the ΔABC,AB=a,AC=candBC=b, then
Aa+b+c=0Ba+b-c=0Ca-b+c=0D−a+b+c=0In a ΔABC, AB = AC and D is a point on AB, such that AD = DC = BC. Then, ∠BAC is
A40∘B45∘C30∘D36∘In a △ABC,AB = AC and AD⊥BC, then :
AAB<ADBAB>ADCAB=ADDAB≤AD
In ΔABC,AB=AC and D is a point in BC so that BD=CD. Prove that AD bisects ∠BAC.
View SolutionIn ΔABC, AB=10, AC=7, BC=9, then find the length of the median drawn from point Cto side AB.
View SolutionD is the midpoint of side BC of ΔABC. If AB=4, AC=6 and BC=8, then find l(AD) and hence perimeter of ΔABD.
View SolutionIn ΔABC, if BC>AC>AB then :
(i) What is the relation ∠A and ∠C ?
(ii) What is the relation between the values of (AB+AC) and BC ?
(iii) What is the relation between the values of (AC−BC) and AB ?
(iv) What is the smallest angle in ΔABC ?
View SolutionIn △ABC, AB=AC and AD⊥BC,BE⊥AC and CF⊥AB. Then △ABC is symmetrical about
View Solution