In a right angled ΔABC,∠C=90∘andCD is the perpendicular on the hypotenuse AB,AB=c,BC=a,AC=bandCD=p, then :
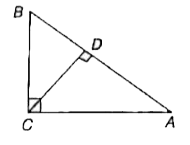
pq=pb
1p2+1b2=1a2
p2=b2+c2
1p2=1a2+1b2
The correct Answer is:D
Step by step video, text & image solution for In a right angled DeltaABC, angleC=90^(@) and CD is the perpendicular on the hypotenuse AB, AB = c, BC = a, AC = b and CD = p, then : by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
- GEOMETRYBook:ARIHANT SSCChapter:GEOMETRYExercise:INTRODUCTORY EXERCISE - 12.3
Explore 28 Videos
- GEOMETRYBook:ARIHANT SSCChapter:GEOMETRYExercise:INTRODUCTORY EXERCISE - 12.4
Explore 10 Videos
- GEOMETRYBook:ARIHANT SSCChapter:GEOMETRYExercise:INTRODUCTORY EXERCISE - 12.1
Explore 45 Videos
- FUNDAMENTALS Book:ARIHANT SSCChapter:FUNDAMENTALS Exercise:TEST OF YOU - LEARNING - 2
Explore 40 Videos
- HCF AND LCMBook:ARIHANT SSCChapter:HCF AND LCMExercise:Exercise Higher Skill Level Questions
Explore 18 Videos
Similar Questions
Knowledge Check
In a right angled ΔABC,∠C=90∘andCD is the perpendicular on hypotenuse AB if BC = 15 cm and AC=20cm then CD is equal to :
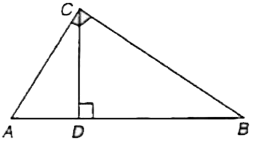 A18 cmB12 cmC17.5 cmDcan't be determined
A18 cmB12 cmC17.5 cmDcan't be determinedIn a right angled triangle ABC, CD is the perpendicular on the hypotenuse AB. Which of the following is correct?
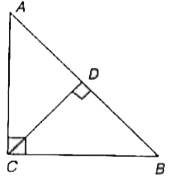 ACD=AC×BCABBAD=AC×ACABCBD=BC×BCABDAll of the above
ACD=AC×BCABBAD=AC×ACABCBD=BC×BCABDAll of the aboveIn ΔABC,∠C=90∘ and CD is perpendicular to AB at D. If ADBD=√k, then ACBC=?
Aa)kBb)√kCc)1√kDd)4√k
In a right-angled triangle ABC ,D is the foot of the perpendicular from B on the hypotenuse AC . If AB=3cm and BC=4cm, what is the area of △ABD?
View SolutionΔABC is right angle triangle where ∠ABC=90∘ and BN is perpendicular to AC. Here, AB= 6 cm., AC = 10 cm. then find AN : NC?
View SolutionABC is a right angle triangle at A and AD is perpendicular to the hypotenuse. Then BDCD is equal to :
View SolutionABC is a right angle triangle at A and AD is perpendicular to the hypotenuse. Then BDCD is equal to :
View SolutionIn right angled ΔABC,∠B=90∘, if P and Q are points on the sides AB and BC respectively, then :

View Solution