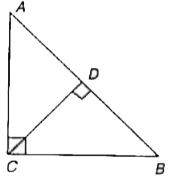
ABC is a right angle triangle at A and AD is perpendicular to the hypotenuse. Then $\frac{B D}{C D}$ is equal to :

A

${(\frac{A B}{A C})}^{2}$

B

${(\frac{A B}{A D})}^{2}$

C

$\frac{A B}{A C}$

D

$\frac{A B}{A D}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

|

Answer

Step by step video, text & image solution for ABC is a right angle triangle at A and AD is perpendicular to the hypotenuse. Then (BD)/(CD) is equal to : by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.

Updated on:21/07/2023

Class 14 MATHS GEOMETRY

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
ABC is a right angle triangle at A and AD is perpendicular to the hypotenuse. Then $\frac{B D}{C D}$ is equal to :
A ${(\frac{A B}{A C})}^{2}$
B ${(\frac{A B}{A D})}^{2}$
C $\frac{A B}{A C}$
D $\frac{A B}{A D}$
Question 2 - Select One
ABC is a triangle right angled at Aand a perpendicular AD is drawn on the hypotenuse BC. What is BC.AD equal to ?
AAB .AC
BAB . AD
CCA .CD
DAD . DB
Question 3 - Select One
ABC is a triangle which is right angled at A and a perpendicular AD is drawn on the hypotenuse BC. If BC = 8 and AD = 3, then what is the value of $A B \times A C$ ?
A12
B24
C32
D36

ARIHANT SSC-GEOMETRY-INTRODUCTORY EXERCISE - 12.2

Home
Ask Doubt
Profile