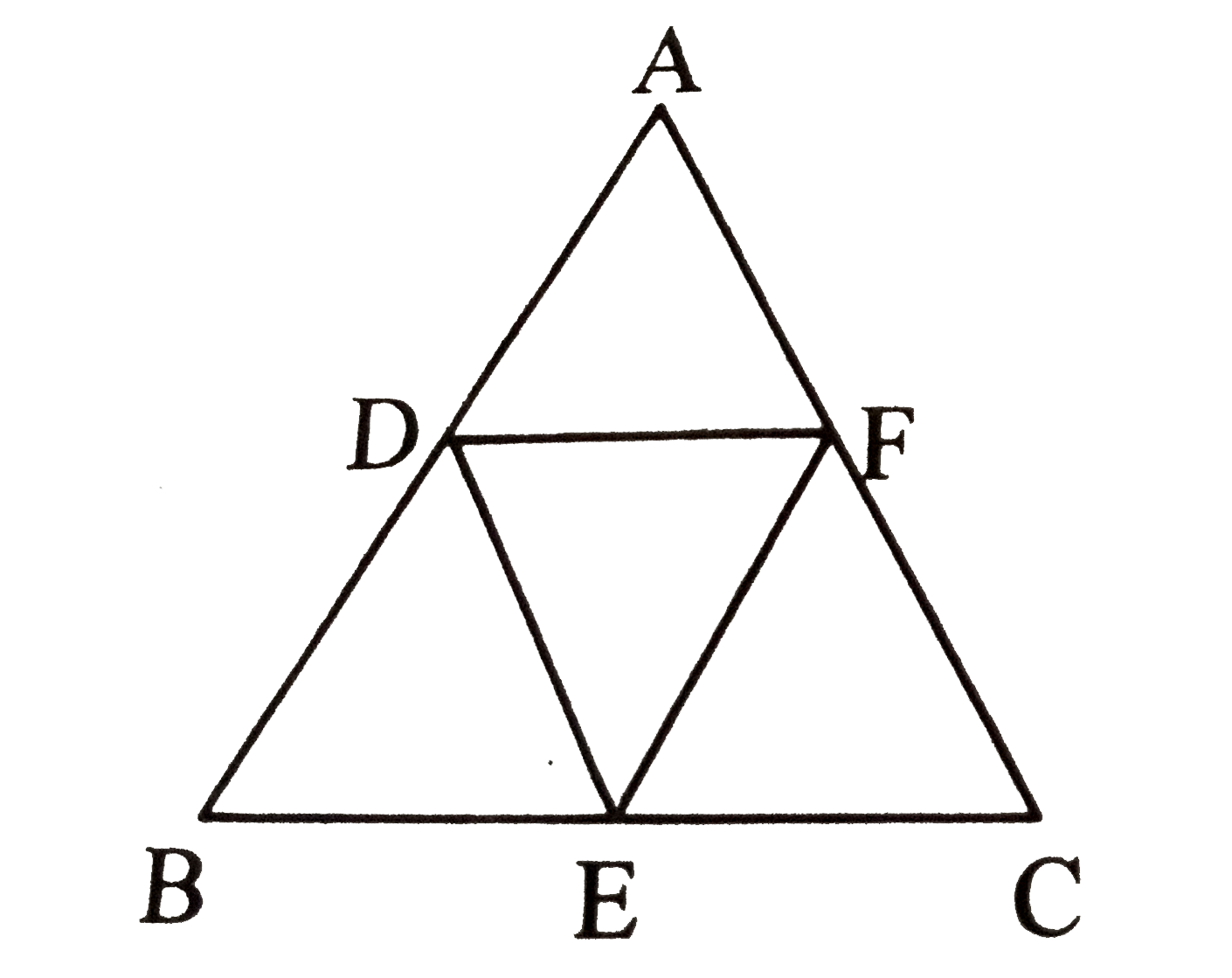
If D, E and F are respectively the mid - points of sides BC, AC and AB of a ΔABC. If EF=3cm,FD=4cm and AB=10cm, then DE,BCandCA respectively will be equal to :
6, 8 and 20 cm
4, 6 and 8 cm
5, 6 and 8 cm
103, 9 and 12 cm
The correct Answer is:C
To solve the problem step by step, we will use the Midpoint Theorem and properties of similar triangles.
Step 1: Understand the given information
We have triangle ABC with midpoints D, E, and F on sides BC, AC, and AB respectively. We are given:
- EF = 3 cm
- FD = 4 cm
- AB = 10 cm
Step 2: Use the Midpoint Theorem
According to the Midpoint Theorem, if D, E, and F are midpoints of sides BC, AC, and AB respectively, then:
- DE is parallel to AB
- EF is parallel to AC
- FD is parallel to BC
Step 3: Find DE
Since DE is parallel to AB and D and E are midpoints, we can use the ratio of the sides:
- Since AB = 10 cm, and DE is half of AB, we can calculate DE as follows:
DE=AB2=10 cm2=5 cm
Step 4: Find BC
Next, we need to find the length of BC. We know that:
- EF is parallel to AC, and since E and F are midpoints, we can use the ratio of the sides again:
Using the triangle AFE and triangle ABC, we have:
AFAB=EFBC
Since AF is half of AB (because F is the midpoint), we have:
12=3 cmBC
Cross-multiplying gives:
BC=3 cm×2=6 cm
Step 5: Find CA
Now we need to find CA. We can use triangle BFD and triangle BAC:
BFBA=DFCA
Since BF is half of BA (because F is the midpoint), we have:
12=4 cmCA
Cross-multiplying gives:
CA=4 cm×2=8 cm
Final Results
Now we have:
- DE = 5 cm
- BC = 6 cm
- CA = 8 cm
Thus, the lengths of DE, BC, and CA are 5 cm, 6 cm, and 8 cm respectively.
Summary of Results
The values are:
- DE = 5 cm
- BC = 6 cm
- CA = 8 cm
We have triangle ABC with midpoints D, E, and F on sides BC, AC, and AB respectively. We are given:
- EF = 3 cm
- FD = 4 cm
- AB = 10 cm
According to the Midpoint Theorem, if D, E, and F are midpoints of sides BC, AC, and AB respectively, then:
- DE is parallel to AB
- EF is parallel to AC
- FD is parallel to BC
Since DE is parallel to AB and D and E are midpoints, we can use the ratio of the sides:
- Since AB = 10 cm, and DE is half of AB, we can calculate DE as follows:
DE=AB2=10 cm2=5 cm
Next, we need to find the length of BC. We know that:
- EF is parallel to AC, and since E and F are midpoints, we can use the ratio of the sides again:
Using the triangle AFE and triangle ABC, we have:
AFAB=EFBC
Since AF is half of AB (because F is the midpoint), we have:
12=3 cmBC
Cross-multiplying gives:
BC=3 cm×2=6 cm
Now we need to find CA. We can use triangle BFD and triangle BAC:
BFBA=DFCA
Since BF is half of BA (because F is the midpoint), we have:
12=4 cmCA
Cross-multiplying gives:
CA=4 cm×2=8 cm
Now we have:
- DE = 5 cm
- BC = 6 cm
- CA = 8 cm
The values are:
- DE = 5 cm
- BC = 6 cm
- CA = 8 cm
Topper's Solved these Questions
- GEOMETRYBOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - INTRODUCTORY EXERCISE - 12.3
28 Videos
- GEOMETRYBOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - INTRODUCTORY EXERCISE - 12.4
10 Videos
- GEOMETRYBOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - INTRODUCTORY EXERCISE - 12.1
45 Videos
- FUNDAMENTALS BOOK - ARIHANT SSCCHAPTER - FUNDAMENTALS EXERCISE - TEST OF YOU - LEARNING - 2
40 Videos
- HCF AND LCMBOOK - ARIHANT SSCCHAPTER - HCF AND LCMEXERCISE - Exercise Higher Skill Level Questions
18 Videos
Similar Questions
Knowledge Check
If D, E and F are respectively the mid - points of sides BC, AC and AB of a ΔABC. If EF=3cm,FD=4cm and AB=10cm, then DE,BCandCA respectively will be equal to :
A6, 8 and 20 cmB4, 6 and 8 cmC5, 6 and 8 cmD10/3, 9 and 12 cmIn a ΔABC,D,EandF are respectively the mid-points of BC, CA and AB. If the lengths of side AB, BC and CA are 7 cm, 8 cm and 9 cm respectively, find the permeter of ΔDEF.
A13 cmB10 cmC12 cmD11 cm
Points D, E and F are the midpoints of sides AB, BC, and AC of ΔABC . If DE = 10 cm, EF = 12 cm and DF = 8 cm, then find AB.
View SolutionD, E and F are respectively the mid-points of the sides BC, CA and AB of a ΔABC. Show that
ar(△DEF)=14ar(△ABC)
View SolutionD, E and F are respectively the mid -points of the sides BC, CA and AB of a △ABC .Show that (i) BDEF is a parallelogram
View SolutionD, E and F are respectively the mid-points of sides AB. BC and CA of △ABC. Find the ratio of the areas of △DEF and △ABC.
View SolutionDandE are respectively the points on the side ABandAC of a ABC such that AB=5.6cm,AD=1.4cm,AC=7.2cm and AE=1.8cm, show that DEBC.
View SolutionIf D and E are respectively the midpoints of the sides AB and BC of △ABC in which AB = 7.2 cm, BC = 9.8 cm and AC = 3.6 cm then determine the length of DE.
View Solution
