If D and E are respectively the midpoints of the sides AB and BC of △ABC in which AB = 7.2 cm, BC = 9.8 cm and AC = 3.6 cm then determine the length of DE.
The correct Answer is:1.8 cm
De is the line joining the midpoints of sides AB and BC of △ABC. So, by midpoint theorem,
DE=12AC=(12×3.6)cm=1.8cm.
Related Playlists
- BOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - MULTIPLE-CHOICE QUESTIONS (MCQ)9videos
QUADRILATERALS
- BOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - Short-Answer Questions1videos
QUADRILATERALS
- BOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - EXERCISE 10C18videos
QUADRILATERALS
- BOOK - RS AGGARWALCHAPTER - PROBABILITYEXERCISE - Multiple Choice Questions (Mcq)16videos
PROBABILITY
- BOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - MULTIPLE-CHOICE QUESTIONS (MCQ)10videos
TRIANGLES
Similar Questions
D and E are respectively the points on the sides AB and AC of a triangle ABC such that AE = 5 cm, AC= 7.5 cm, DE= 4.2 cm and DE||BC. Then find length of BC.
View SolutionD and E are respectively the points on the sides AB and AC of a triangle ABC such that AD=2cm, BD=3cm,BC=7.5cm and DE || BC. Then length of DE (in cm) is
(a) 2.5
(b) 3
(c) 5
(d) 6View SolutionCan we construct a triangle ABC in which AB=3 cm, BC=4 cm and AC=8 cm ?
View SolutionIf D, E and F are respectively the mid - points of sides BC, AC and AB of a ΔABC. If EF=3cm,FD=4cm and AB=10cm, then DE,BCandCA respectively will be equal to :
View SolutionConstruct a circumcircle for the triangle ABC in which AB = 3 cm, BC = 3 . 5 cm, and AC = 3.5 cm
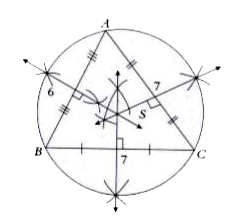 View Solution
View SolutionDandE are respectively the points on the side ABandAC of a ABC such that AB=5.6cm,AD=1.4cm,AC=7.2cm and AE=1.8cm, show that DEBC.
View SolutionProve xa>yb if x>y and b<0 .
View SolutionIn △ABC, AB = 6 cm, AC = 8 cm, and BC = 9 cm. The length of median AD is:
View SolutionIn a right-angled triangle ABC, if angle B=90°, BC = 3 cm and AC = 5 cm, then the length of side AB is
View SolutionConstruct a triangle ABC in which BC = 8cm, ∠B=45∘ and AB - AC = 3.5 cm.
View Solution


