Is quadrilateral a ||gm?
I. Diagonals and bisect each other.
II. Diagonals and are equal.
if the question can be answered by one of the given statements alone and not by the other,
if the quesiton can be answered by either statement alone,
if the question can be answered by both the statements together but not by any one of the two,
if the question cannot be answered by using both the statements together.
The correct Answer is:A
We know that if the diagonals of a quadrilateral bisect each other then it is a ||gm.
I gives the answer.
If the diagonals of a quadrilateral are equal then it is not necessarily a ||gm.
II does not give the answer.
Hence, the correct answer is (a).
Topper's Solved these Questions
- QUADRILATERALSBOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - MULTIPLE-CHOICE QUESTIONS (MCQ)
9 Videos
- QUADRILATERALSBOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - Short-Answer Questions
1 Videos
- QUADRILATERALSBOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - EXERCISE 10C
18 Videos
- PROBABILITYBOOK - RS AGGARWALCHAPTER - PROBABILITYEXERCISE - Multiple Choice Questions (Mcq)
16 Videos
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - MULTIPLE-CHOICE QUESTIONS (MCQ)
10 Videos
Similar Questions
Knowledge Check
Is quadrilateral ABCD a rhombus ?
I. Quadrilateral ABCD is a ||gm.
II. Diagonals AC and BD are perpendicular to each other.Aif the question can be answered by one of the given statements alone and not by the other,Bif the quesiton can be answered by either statement alone,Cif the question can be answered by both the statements together but not by any one of the two,Dif the question cannot be answered by using both the statements together.In a quadrilateral ABCD, with unequal sides if the diagonals AC and BD intersect at right angles, then
AAB2+BC2=CD2+DA2BAB2+CD2=BC2+DA2CAB2+AD2=BC2+CD2DAB2+BC2=2(CD2+DA2)In a quadrilateral ABCD, with unequal sides if the diagonals AC and BD intersect at right angles, then
AAB2+BC2=CD2+DA2BAB2+CD2=BC2+DA2CAB2+AD2=BC2+CD2DAB2+BC2=2(CD2+DA2)
Two segments AC and BD bisect each other at O . Prove that ABCD is a parallelogram.
View SolutionIn a quadrilateral ABCD, it is given that AB∣∣CD and the diagonals ACandBD are perpendicular to each other. Show that AD.BC≥AB.CD.
View SolutionIn Quadrilateral ABCD, diagonal AC & BD intersect at "O". By Diagonals area of quadrilateral ABCD is divided into 4 parts. Find area of the fourth part (x), area of other 3 parts is mentioned in the figure.
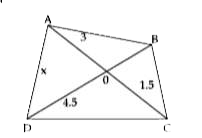
View SolutionIn cyclic quadrilateral ABCD, Diagonals AC and BD intersect at P. If ∠DBC=70∘ and ∠BAC=30∘ then find ∠BCD
View SolutionABCD is a cycle quadrilateral. Diagonals BD and AC intersect each other at E. If ∠BEC=128∘ and ∠ECD=25∘ then what is the measure of ∠BAC ?
View Solution

