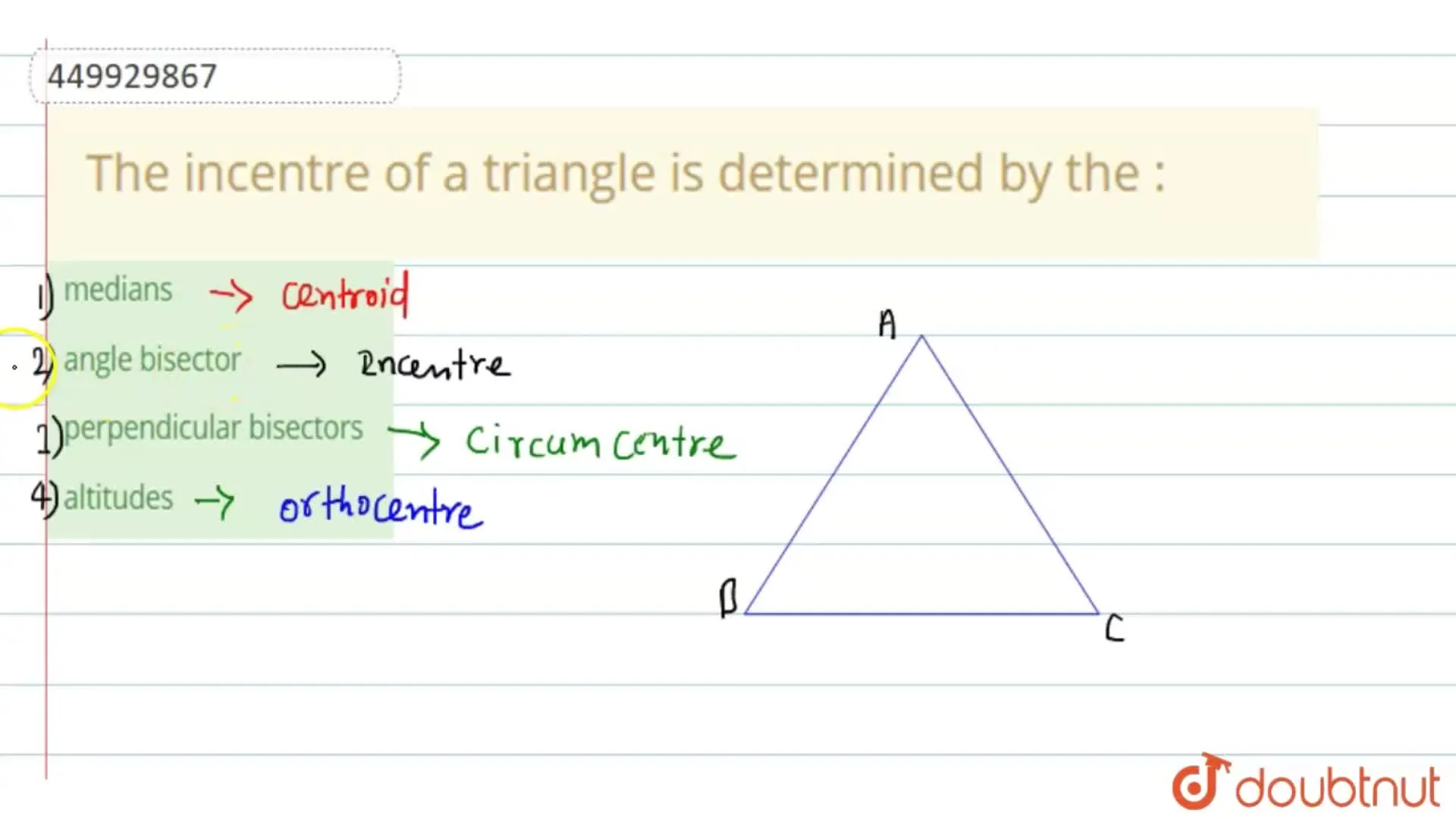
The incentre of a triangle is determined by the :
medians
angle bisector
perpendicular bisectors
altitudes
The correct Answer is:B
Step by step video, text & image solution for The incentre of a triangle is determined by the : by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Related Playlists
- BOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - INTRODUCTORY EXERCISE - 12.328videos
GEOMETRY
- BOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - INTRODUCTORY EXERCISE - 12.410videos
GEOMETRY
- BOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - INTRODUCTORY EXERCISE - 12.145videos
GEOMETRY
- BOOK - ARIHANT SSCCHAPTER - FUNDAMENTALS EXERCISE - TEST OF YOU - LEARNING - 240videos
FUNDAMENTALS
- BOOK - ARIHANT SSCCHAPTER - HCF AND LCMEXERCISE - Exercise Higher Skill Level Questions18videos
HCF AND LCM
Similar Questions
The incentre of the triangle formed by the lines y=|x| and y=1 is
View SolutionThe incentre of the triangle formed by the coordinates axes and 3x+4y=12 is
View SolutionThe incentre of the triangle formed by the points i+j+k,4i+j+k,4i+5j+k is
View SolutionThe incentre of the triangle formed by the points (3,0,4),(0,4,4),(0,0,4) is
View SolutionThe incentre of the triangle formed by the line 3x+4y−12=0 with the coordinate axis is
View Solution" The incentre of the triangle formed by the points "(3,0,4)*(0,4,4),(0,0,4)" is "
View SolutionThe incentre of the triangle formed by the straight line having 3 as X-intercept and 4 as Y-intercept, together with the coordinate axes, is
View SolutionThe incentre of the triangle formed by the lines y=√3x,y=−√3x and y=3 is
View SolutionIf (x, y) is the incentre of the triangle formed by the points (3, 4), (4, 3) and (1, 2), then the value of x2 is
View SolutionThe incentre of a triangle coincides with the circumcentre, orthocentre and centroid in case of :
View Solution