The four triangles formed by joining the pairs of mid - points of the sides of a given triangle are congruent if the given triangle is :
an isosceles triangle
an equilateral triangle
a right angled triangle
of any shape
The correct Answer is:D
To determine when the four triangles formed by joining the pairs of midpoints of the sides of a given triangle are congruent, we can follow these steps:
Step 1: Understand the Problem
We start with a triangle ABC. We need to find out under what conditions the triangles formed by joining the midpoints of the sides of triangle ABC are congruent.
Hint: Think about the properties of triangles and how midpoints affect the sides.
Step 2: Identify the Midpoints
Let D, E, and F be the midpoints of sides AB, BC, and CA respectively. By connecting these midpoints, we form four smaller triangles: ADF, BDE, CEF, and DEF.
Hint: Visualize or sketch the triangle and label the midpoints clearly.
Step 3: Analyze the Congruence of Triangles
To check if triangles ADF, BDE, CEF, and DEF are congruent, we need to consider their sides and angles.
1. Side Lengths: Since D, E, and F are midpoints, the segments AD, DF, BE, and EF are all half the lengths of the corresponding sides of triangle ABC.
2. Angles: The angles at each vertex of the smaller triangles depend on the angles of triangle ABC.
Hint: Use the properties of congruent triangles (SSS, SAS, ASA) to analyze the relationships.
Step 4: Determine Conditions for Congruence
For the triangles ADF and BDE to be congruent:
- They must have equal corresponding sides and angles.
This is guaranteed when triangle ABC is equilateral because:
- All sides are equal, and all angles are equal (60 degrees each).
- Thus, the triangles formed by the midpoints will also be equal in size and shape.
Hint: Consider the implications of having equal angles and sides in triangle ABC.
Step 5: Conclusion
The four triangles formed by joining the pairs of midpoints of the sides of triangle ABC are congruent if triangle ABC is an equilateral triangle.
Final Answer: The given triangle must be an equilateral triangle.
We start with a triangle ABC. We need to find out under what conditions the triangles formed by joining the midpoints of the sides of triangle ABC are congruent.
Let D, E, and F be the midpoints of sides AB, BC, and CA respectively. By connecting these midpoints, we form four smaller triangles: ADF, BDE, CEF, and DEF.
To check if triangles ADF, BDE, CEF, and DEF are congruent, we need to consider their sides and angles.
2. Angles: The angles at each vertex of the smaller triangles depend on the angles of triangle ABC.
For the triangles ADF and BDE to be congruent:
- They must have equal corresponding sides and angles.
- All sides are equal, and all angles are equal (60 degrees each).
- Thus, the triangles formed by the midpoints will also be equal in size and shape.
The four triangles formed by joining the pairs of midpoints of the sides of triangle ABC are congruent if triangle ABC is an equilateral triangle.
Topper's Solved these Questions
- GEOMETRYBook:ARIHANT SSCChapter:GEOMETRYExercise:INTRODUCTORY EXERCISE - 12.3
Explore 28 Videos
- GEOMETRYBook:ARIHANT SSCChapter:GEOMETRYExercise:INTRODUCTORY EXERCISE - 12.4
Explore 10 Videos
- GEOMETRYBook:ARIHANT SSCChapter:GEOMETRYExercise:INTRODUCTORY EXERCISE - 12.1
Explore 45 Videos
- FUNDAMENTALS Book:ARIHANT SSCChapter:FUNDAMENTALS Exercise:TEST OF YOU - LEARNING - 2
Explore 40 Videos
- HCF AND LCMBook:ARIHANT SSCChapter:HCF AND LCMExercise:Exercise Higher Skill Level Questions
Explore 18 Videos
Similar Questions
Knowledge Check
Any two of the four triangles formed by joining the mid - points of the sides of a given triangle are :
AcongruentBequal in area but not congruentCunequal in area and not congruentDnone of the aboveAny two of the four triangles formed by joining the mid - points of the sides of a given triangle are :
AcongurentBequal in area but not congruentCunequal in area and not congruentDnone of the aboveWhich of the following triangles is congruent to the given triangle?
 A
A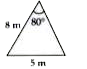 B
B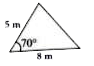 C
C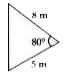 D
D
The four triangles formed by joining the midpoints of the sides of a given triangle are equal in area: each equal to one-fourth of given triangle.
View SolutionShow that the given triangles are congruent.

View SolutionA triangle is formed by joining the mid- points of the sides of a given triangle. This process is continued indefinitely. All such triangles formd are similar to one another. (True/False).
View SolutionOne side of an equilateral triangle is 36 cm. The mid-points of its sides are joined to form another triangle. Again another triangle is formed by joining the mid-points of the sides of this triangle and the process is continued indefinitely. Determine the sum of areas of all such triangles including the given triangle.
View SolutionA triangle PQR is formed by joining the mid-points of the sides of a triangle ABC. 'o' is the circumcentre of △ABC, then for △PQR, the point 'o' is :
View Solution
