In a ΔABC,D is the mid - point of BC and E is mid - point of AD, BF passes through E. What is the ratio of AF:FC?
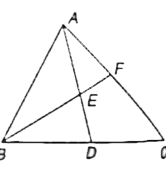
1:1
1:2
1:3
2:3
The correct Answer is:B
Step by step video, text & image solution for In a DeltaABC, D is the mid - point of BC and E is mid - point of AD, BF passes through E. What is the ratio of AF:FC? by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
- GEOMETRYBOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - INTRODUCTORY EXERCISE - 12.3
28 Videos
- GEOMETRYBOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - INTRODUCTORY EXERCISE - 12.4
10 Videos
- GEOMETRYBOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - INTRODUCTORY EXERCISE - 12.1
45 Videos
- FUNDAMENTALS BOOK - ARIHANT SSCCHAPTER - FUNDAMENTALS EXERCISE - TEST OF YOU - LEARNING - 2
40 Videos
- HCF AND LCMBOOK - ARIHANT SSCCHAPTER - HCF AND LCMEXERCISE - Exercise Higher Skill Level Questions
18 Videos
Similar Questions
In ΔABC, D is the midpoint of side BC, E is mid point of AD, F is midpoint of BE and G is mid-point of FC. What part of the area of ΔABC is the area of ΔEFG?
View SolutionIn ΔABC,D is the mid-pointpoint of BC and E is mid-point of AD.BE is produced to meet the side AC in F.Then BF is equal to
View Solution
Knowledge Check
In ΔABC,D is the mid-point of BC . Length AD is 27 cm . N is a point in AD such that the length of DN is 12 cm . The distance of N from the centroid of ΔABC is equal to
A3 cmB6 cmC9 cmD15 cmIn a ΔABC,D,E,F are the mid -points of the sides BC, CA and AB respectively, the vector AD is equal to
A−−→BE+−−→CFB−−→BE−−−→CFC−−→CF−−−→BED−−−→BE−−−→CF
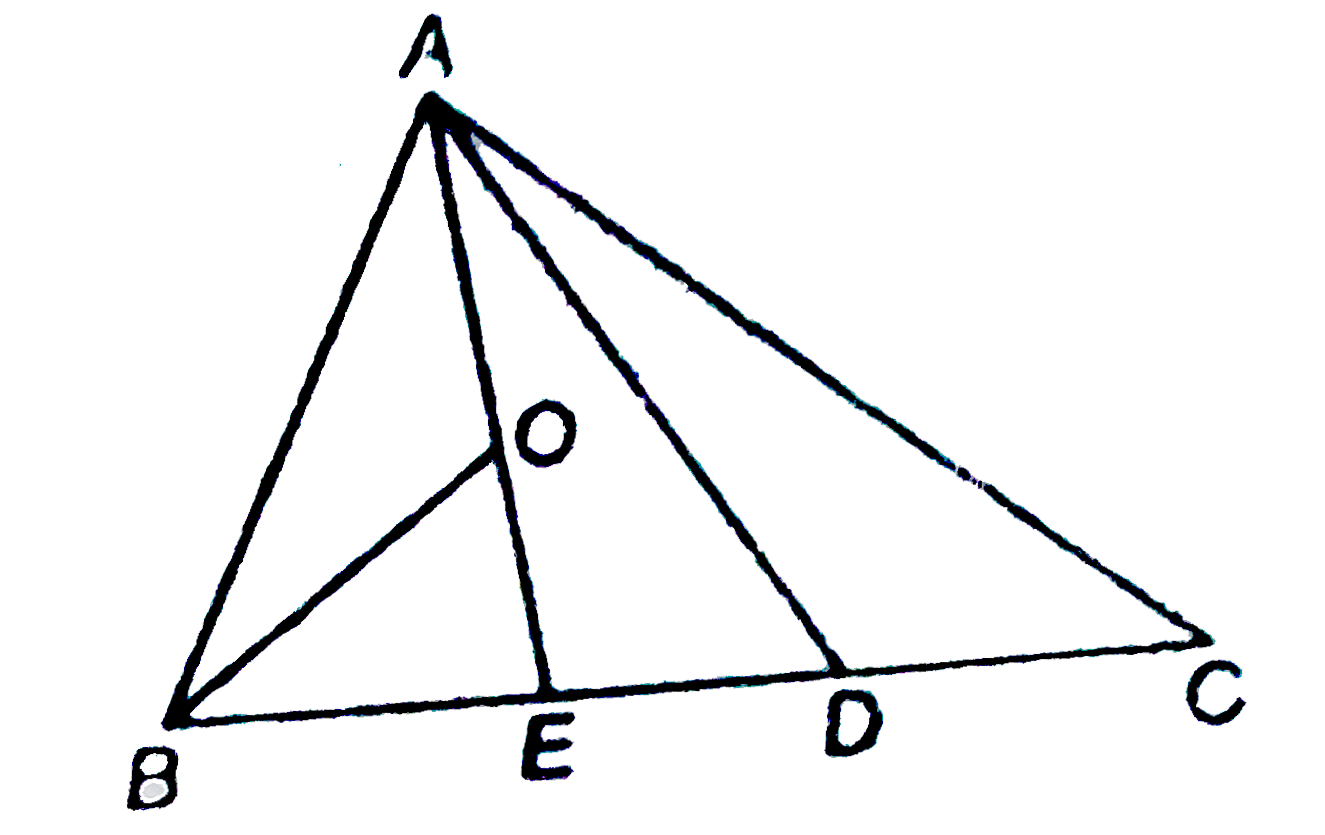
In the given figure, D is the mid-point of BC, E is the mid-point of BD and O is the mid-point of AE. Find the ratio of area of ΔBOEandΔABC
View SolutionIn parallelogram ABCD, E is the mid-point of AD and F is the mid-point of BC. Prove that BFDE is a parallelogram.
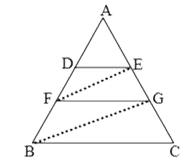
View SolutionIn a ΔABC,DE||EG||BCandEF∣∣BG and D is a midpoint of AF. Find the ratio of area of ΔDEF:ΔABC
View SolutionA(a+1,a−1),B(a2+1,a2−1) and C(a3+1,a3−1) are given points. D (11, 9) is the mid point of AB and E (41, 39) is the mid point of BC. If F is the mid point of AC then (BF)2 is equal to K2, where K =
View SolutionD is the mid-point of side BC of ΔABC and E is the mid-point of BO. If O is the mid-point of AE, then ar(ΔBOE) = 1/k ar(ΔABC). Then k equals
View SolutionD is the mid-point of side BC of ABC and E is the mid-point of BD. If O is the mid-point of AE , prove that ar(BOE)=18ar(ABC)
View Solution
