Question

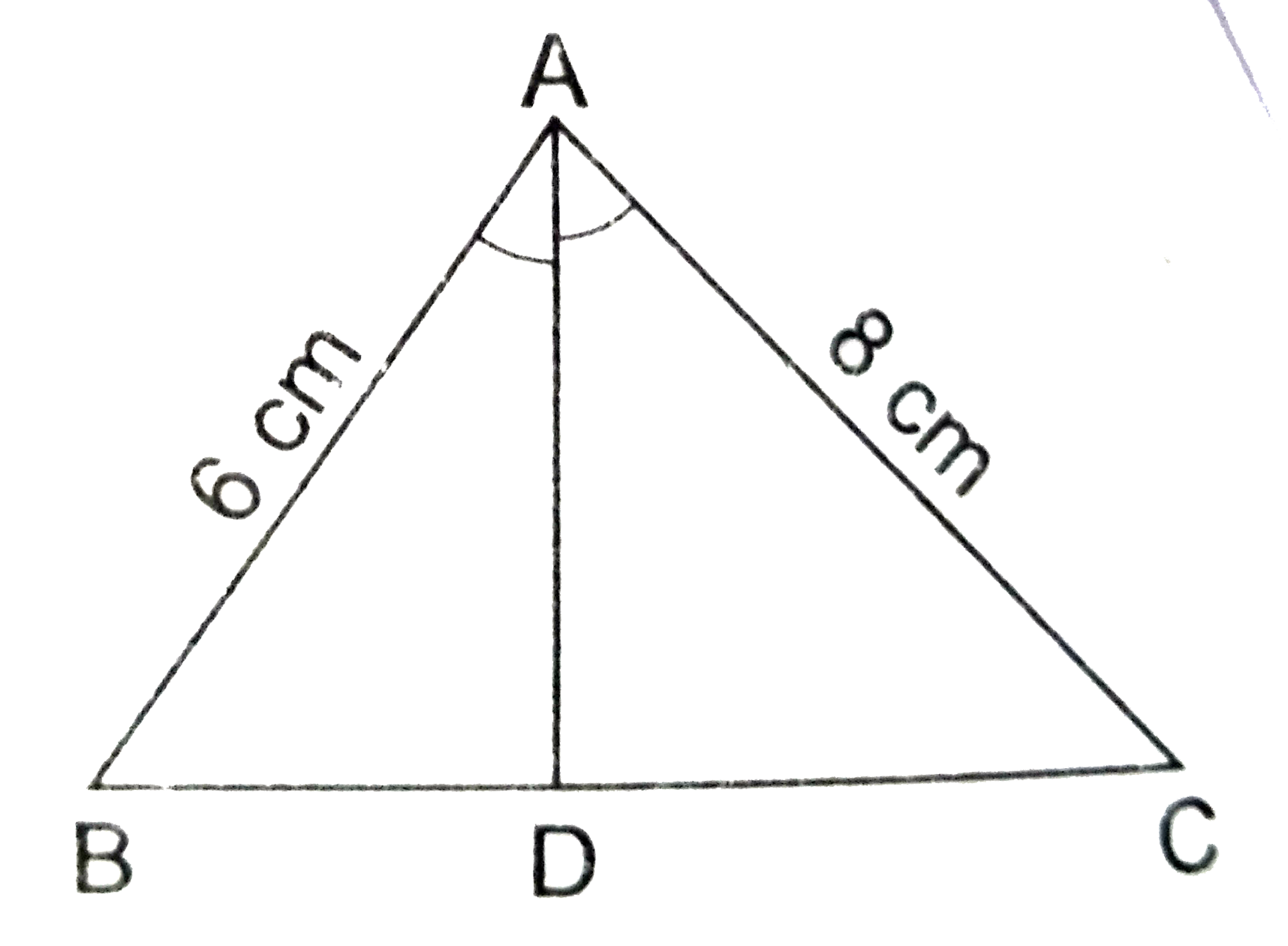
In $\Delta ABC,AB=5cm,AC=7cm$. If AD is the angle bisector of $\angle A$ Then $BD:CD$ is :

Options

A. `25:49`
B. `49:25`
C. `6:1`
D. `5:7`

Answer

D

Explanation

To solve the problem, we will use the Angle Bisector Theorem. According to this theorem, if a point D lies on the side BC of triangle ABC and AD is the angle bisector of angle A, then the following relationship holds:

$$\frac{BD}{CD}=\frac{AB}{AC}$$

1. Identify the given lengths:
- AB = 5 cm
- AC = 7 cm

2. Apply the Angle Bisector Theorem:
- According to the theorem:
\( \frac{BD}{CD} = \frac{AB}{AC} \)
- Substitute the known values:
\( \frac{BD}{CD} = \frac{5}{7} \)

3. Express the ratio:
- This means that the ratio of BD to CD is:
\( BD : CD = 5 : 7 \)

4. Conclusion:
- Therefore, the final answer is:
\( BD : CD = 5 : 7 \)