AB is a line segment of length 48 cm and C is its mid-point. If three semicircles are drawn at AB, AC and CB using as diameters, then radius of the circle inscribed in the space enclosed by three semicircles is
3√2
6
8
10
The correct Answer is:C
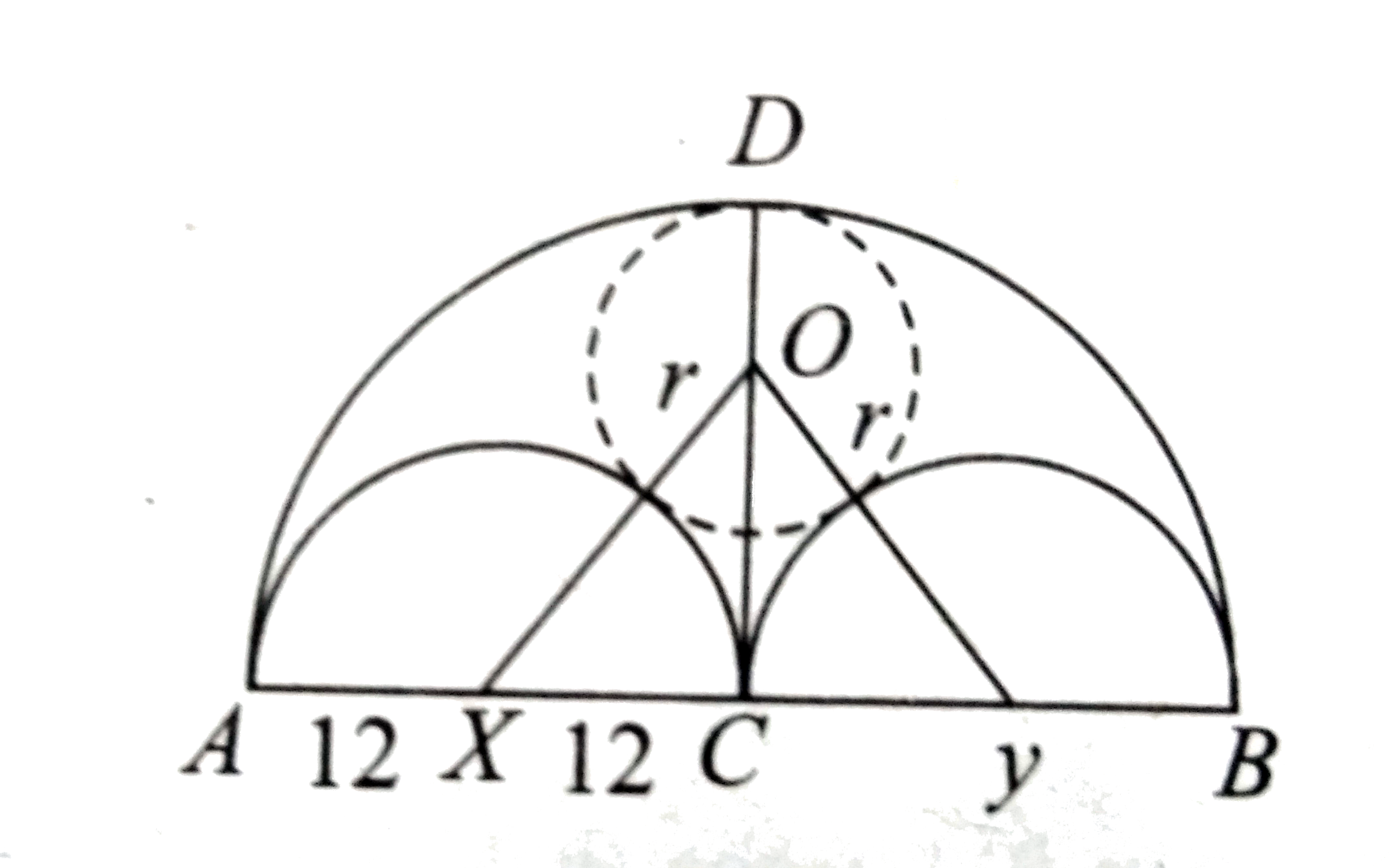
In ΔXCO, we have
OX2+XC2+OC2
⇒(12+r)2=122+(24−r)2
⇒r=8
Topper's Solved these Questions
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank
32 Videos
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Comprehension Type
8 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - JEE Advanced (Single Correct Answer Type)
14 Videos
- COMPLEX NUMBERSBOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - Question Bank
30 Videos
Similar Questions
O is the mid-point of line segment AB of length 36cm. If the semicircles are drawn on AB, OA and OB as diameters, then the radius of the smallest circle which touches all the semicircles is(1) 6 cm (2) 9 cm (3) 12 cm (4) 4 cm.
View SolutionPQ is a lines segment and R is its midpoint. Semicircles are drawn at the same side of PQ taking PR,RQandPQ as diameters. A circle of radius r and centre O is drawn touching all the three semi circles.
Prove that r=16PQ
View Solution
Knowledge Check
AB is the diameter of a semicircle k,C is an arbitrary point on the semicircle (other than A or B) and S is the centre of the circle inscribed into triangle ABC, then measure of-
Aangle ASB changes as C moves on kBangle ASB is the same for all positions of C but it cannot be determined without knowing the radiusCangle ASB=135∘ for all positions of CDangle ASB=150∘ for all positions of C
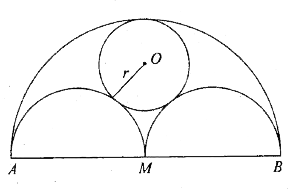
AB is a line segment of length 2a with M as mid-point. Semicircles are drawn on one side with AM, MB and AB as diameter as shown in the above figure. A circle .with centre O and radius r is drawn such that this circle touches all the three semicircles. The value of r is
View SolutionIn Figure AB = 36 cm and M is mid-point of AB. Semi-circles are drawn on AB, AM and MB as diameters. A circle with centre C touches all the three circles. Find the area of the shaded region.
View SolutionABC is a right-angled triangle at A. Semicircles drawn on AB, AC and BC as diameters. Find area of the shaded region.

View SolutionAB is a line segment of length 8 cm. Locate a point C on AB such that AC=13CB.
View SolutionIn Fig 12.58, ABC is a triangle right angled at A. Semicircles are drawn on AB and AC as diameters. Find the area of the shaded region.
View SolutionIn the given figure, ABC is a right angled triangle with B as right angle. Three semicircles are drawn with AB, BC and AC as diameters. What is the area of the shaded portion, if the area of ΔABC is 12 square units ?
View SolutionAB is the diameter of a semicircle k,C is an arbitrary point on the semicircle (other than A or B) and S is the centre of the circle inscribed into triangle ABC, then measure of-
View Solution
