An isosceles triangle with base 24 and legs 15 each is inscribed in a circle with centre at $(- 1, 1)$ . The locus of the centroid of that $Δ$ is

A

$4 (x^{2} + y^{2}) + 8 x - 8 y - 73 = 0$

B

$2 (x^{2} + y^{2}) + 4 x - 4 y - 31 = 0$

C

$2 (x^{2} + y^{2}) + 4 x - 4 y - 21 = 0$

D

$4 (x^{2} + y^{2}) + 8 x - 8 y - 161 = 0$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

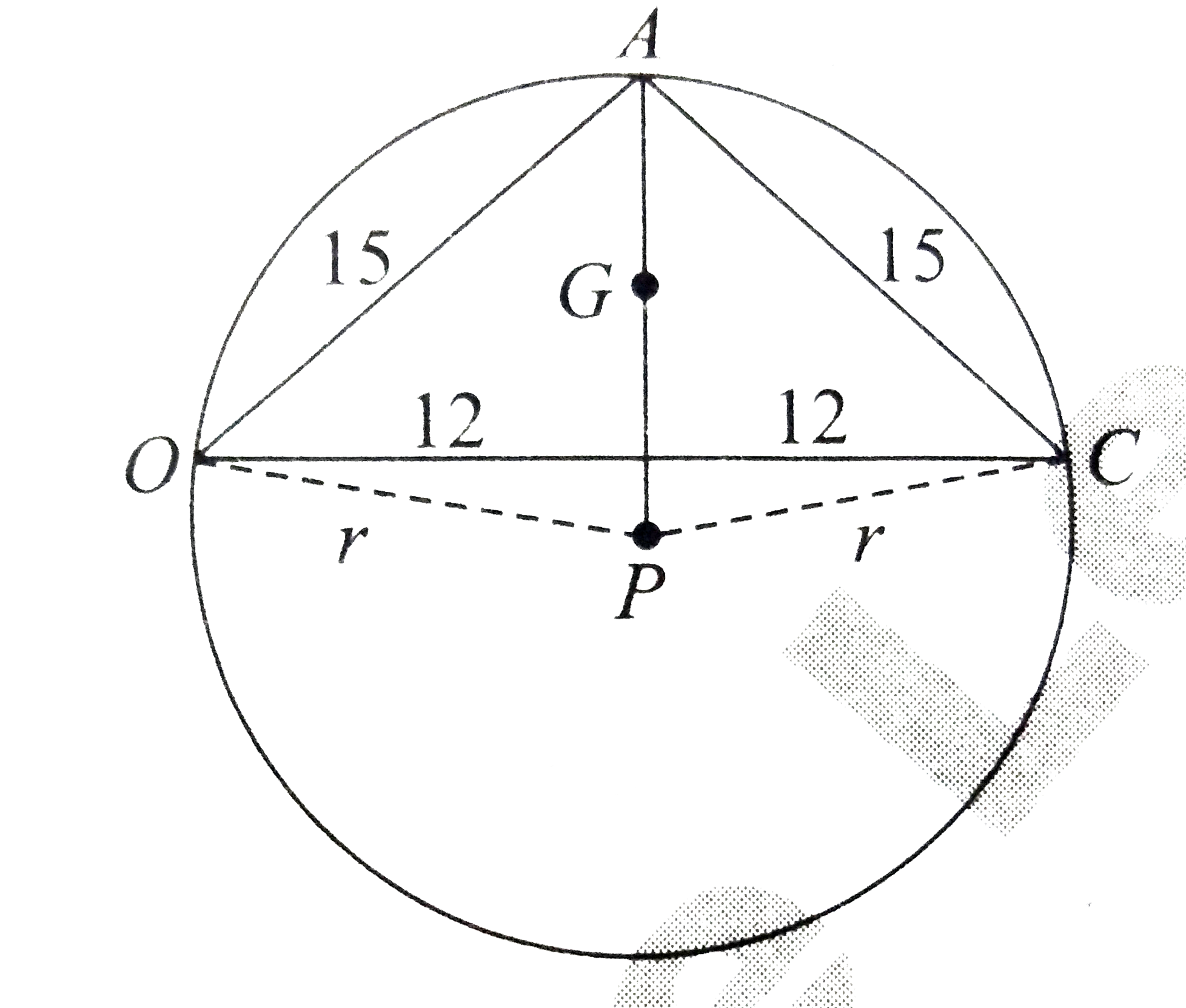
${(r - 9)}^{2} + 12^{2} = r^{2}$
$\Rightarrow 81 - 18 r + 144 = 0$
$\Rightarrow r = \frac{255}{18} = \frac{25}{2}$
Locus is a concentric circle with radius PG.
$P G = (r - 9) + \frac{1}{3} (9)$
$= r - 6$
$= \frac{25}{2} - 6 = \frac{13}{2}$
Lcus is ${(x + 1)}^{2} + {(y - 1)}^{2} = {(\frac{13}{2})}^{2}$
$\Rightarrow x^{2} + y^{2} + 2 x - 2 y - \frac{161}{4} = 0$

|

Updated on:21/07/2023

Class 12 MATHS CIRCLES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The triangle of maximum area inscribed in a circle is :
Aequilateral
Bisosceles
Cright-angled
Dnone of these
Question 2 - Select One
Equilateral $Δ$ ABC is inscribed in a circle with centre P. Then, $∠ B P C$ = ..........
A $60^{\circ}$
B $90^{\circ}$
C $120^{\circ}$
D $75^{\circ}$
Question 3 - Select One
If an equilateral triangle ABC is inscribed in a circle with centre O then the measure of $∠ A O B$ is
A $60^{\circ}$
B $90^{\circ}$
C $120^{\circ}$
D $180^{\circ}$

CENGAGE-CIRCLES-Single Correct Answer Type

Home
Ask Doubt
Profile