A variable line moves in such a way that the product of the perpendiculars from (4, 0) and (0, 0) is equal to 9. The locus of the feet of the perpendicular from (0, 0) upon the variable line is a circle, the square of whose radius is
13
15
19
23
The correct Answer is:A
Let the foot of the perpendicular from origin upon the variable line be (x1,y1).
So, equation of the variable line is:
×1+yy1−(x21+y21)=0
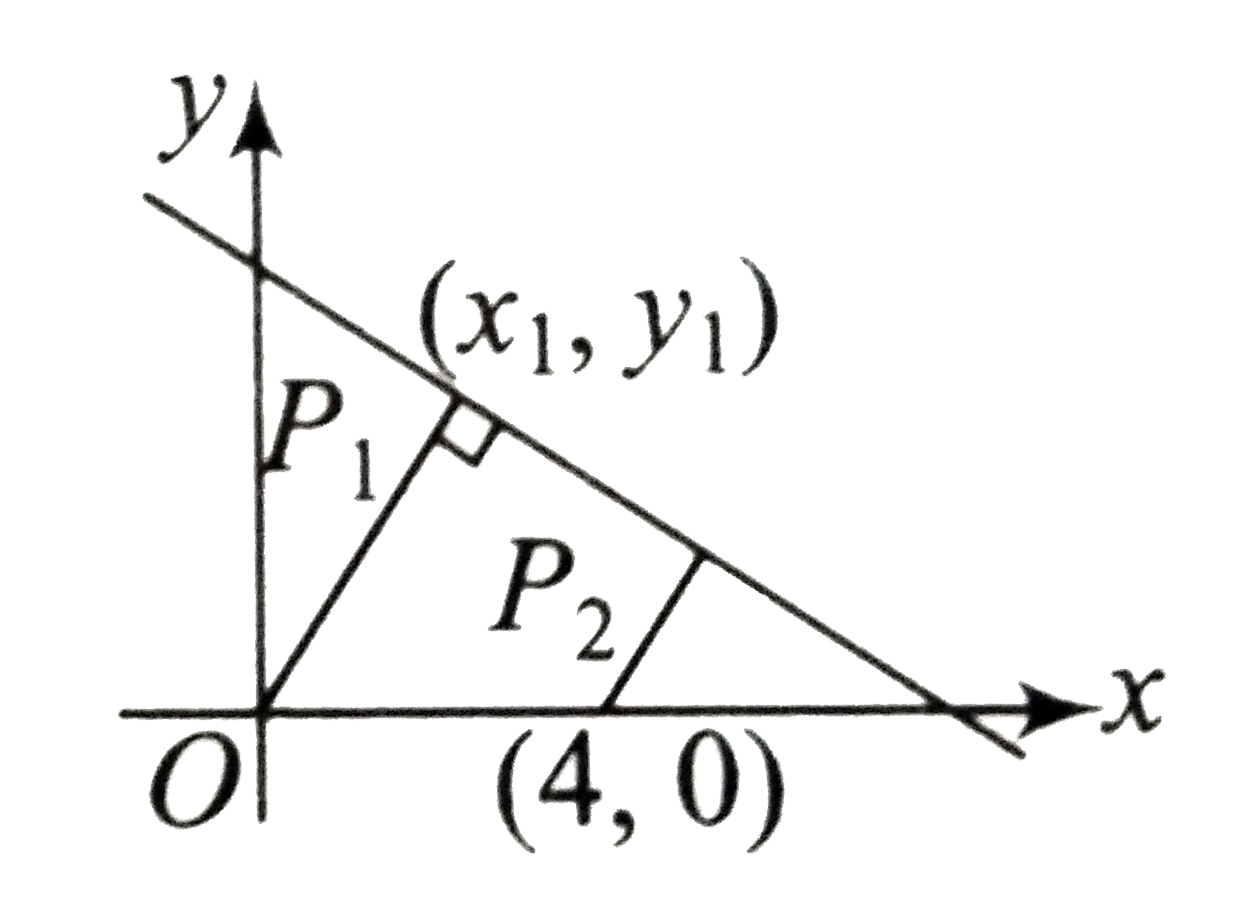
According to the equation,
p1p2=∣∣
∣∣x21+y21√x21+y21∣∣
∣∣∣∣
∣
∣∣4x1−(x21+y21)√x21+y21∣∣
∣
∣∣=9
i.e., ∣∣x21+y21−4x1∣∣=9
Locus is: x2+y2−4x−9=0
∴r2=4+9=13
Topper's Solved these Questions
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank
32 Videos
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Comprehension Type
8 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - JEE Advanced (Single Correct Answer Type)
14 Videos
- COMPLEX NUMBERSBOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - Question Bank
30 Videos
Similar Questions
A variable line moves in a plane such a way that the product of the perpendiculars from A(a, 0) and B(0, 0) is equal to λ2, A and B being on same side of variable line. The locus of the feet of the perpendicular from (0, 0) upon the variable line is a circle which has -
View SolutionThe foot of the perpendicular from (0,0) to the line xcosα+ysinα=p is
View Solution
Knowledge Check
The foot of the perpendicular from (2, 3) upon the line 4x - 5y + 8 = 0 is
A(0, 0)B(1, 1)C(4178,12875)D(7841,12841)The coordinates of the foot of the perpendicular from (a,0) on the line y=mx+am are
A(0,−1a)B(0,am)C(0,−am)D(0,1a)Foot of perpendicular drawn from (0,5) to the line 3x−4y−5=0 is
A(1,3)B(2,3)C(3,2)D(3,1)
Find the locus of the foot of perpendicular from the point (2, 1) on the variable line passing through the point (0, 0).
View SolutionA variable line cuts pair of lines x2−(a+b)x+ab=0 in such a way that intercept between subtends a right angle at origin. The locus of the foot of the perpendicular from origin on variable line is
View SolutionA variable line makes intercepts on the coordinate axes the sum of whose squares is constant and is equal to a . Find the locus of the foot of the perpendicular from the origin to this line.
View SolutionThe locus of foot of the perpendicular drawn from a fixed point (2,3) to the variable line y=mx, m being variable is
View SolutionA straight line moves so that the product of the length of the perpendiculars on it from two fixed points is constant. Prove that the locus of the feet of the perpendiculars from each of these points upon the straight line is a unique circle.
View Solution