In the diagram as shown, a circle is drawn with centre C(1, 1) and radius I and a line L. The line Lis tangential to the circle at Q. Further L meet the y-axis at R and the x-axis at Pis such a way that the angle OPQ equals $θ$ where $0 < θ < \frac{π}{2}$ The coordinates of Q are

A

$(1 + cos θ, 1 + sin θ)$

B

$(sin θ, cos θ)$

C

$(1 + sin θ, cos θ)$

D

$(1 + sin θ, 1 + cos θ)$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

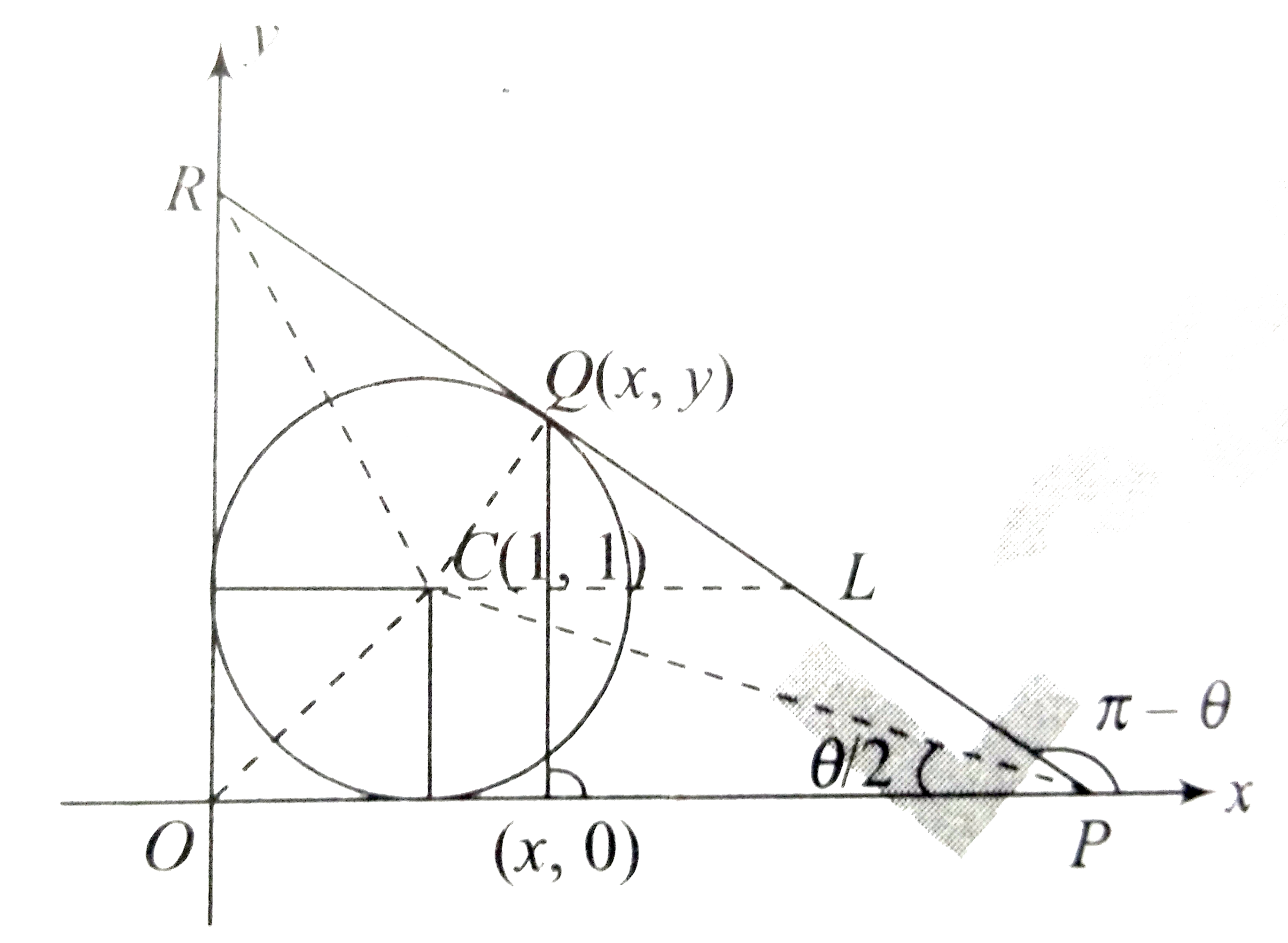
For the circle with center C, using parametric form at straight line, we get
$x - 1 = sin θ$
$y - 1 = cos θ$
Thus, $Q \equiv (1 + sin θ, 1 + cos θ)$

|

Updated on:21/07/2023

Class 12 MATHS CIRCLES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One

In the diagram as shown, a circle is drawn with centre $C (1, 1)$ and radius 1 and a line L. The line L is tangent to the circle at Q. Further L meets the y-axis at R and the x-axis at P in such a way that the angle OPQ equals $θ$ where $0 < θ < \frac{π}{2}$ .
Area of triangle OPR when $θ = π / 4$ is
A $(3 - 2 \sqrt{2})$
B $(3 + 2 \sqrt{2})$
C $(6 + 4 \sqrt{2})$
Dnone of these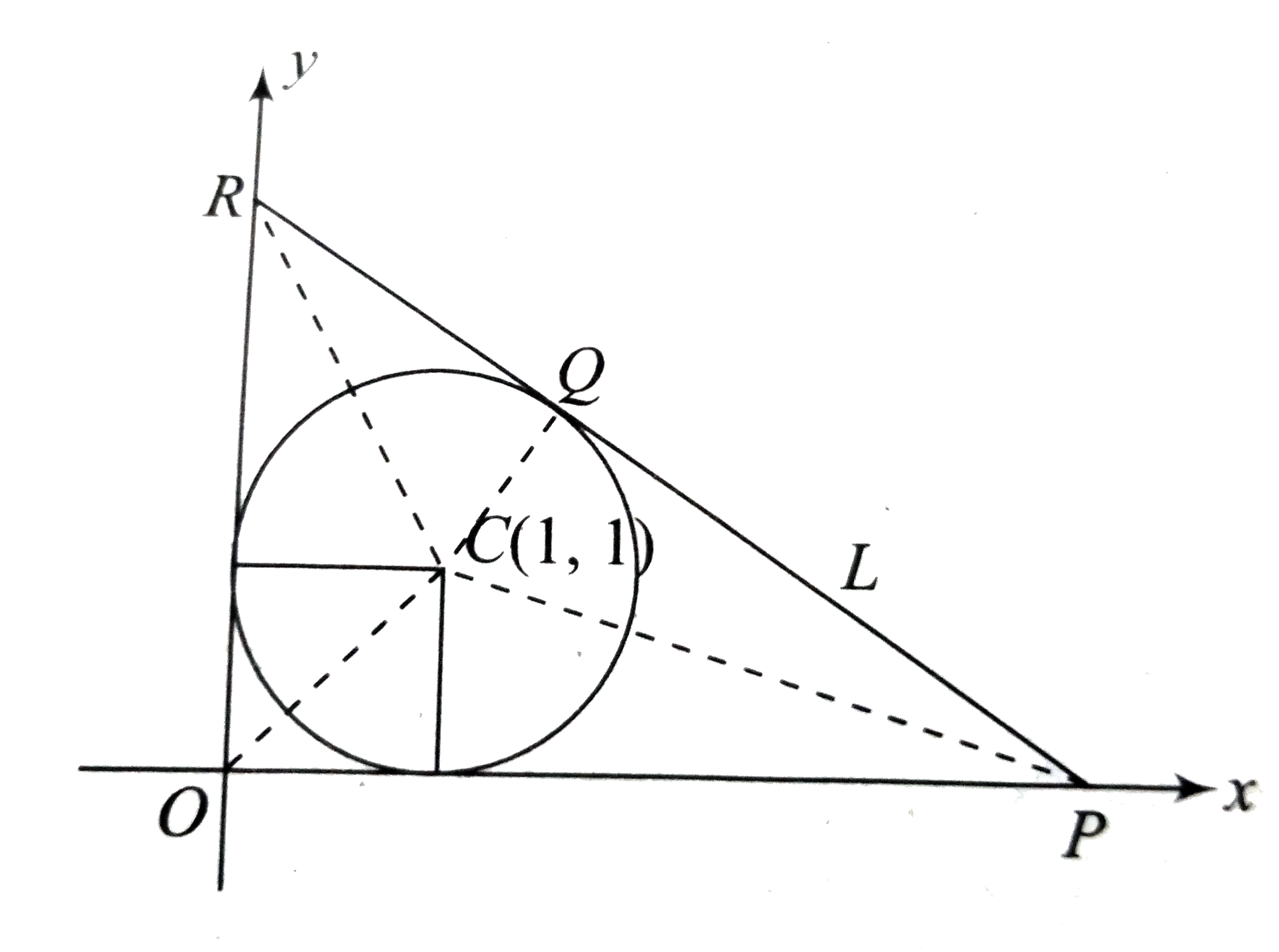
Question 2 - Select One

In the diagram as shown, a circle is drawn with centre $C (1, 1)$ and radius 1 and a line L. The line L is tangent to the circle at Q. Further L meets the y-axis at R and the x-axis at P in such a way that the angle OPQ equals $θ$ where $0 < θ < \frac{π}{2}$ .
Equation of the line PR is
A $x cos θ + y sin θ = sin θ + cos θ + 1$
B $x sin θ + y cos θ = cos θ + sin θ - 1$
C $x sin θ + y cos θ = cos θ + sin θ + 1$
D $x tan θ + y = 1 + cot (\frac{θ}{2})$
Question 3 - Select One
The line $2 x - y + 1 = 0$ is tangent to the circle at the point (2, 5) and the centre of the circle lies on $x - 2 y = 4 .$ The square of the radius of the circle is
A45
B75
C20
D50

CENGAGE-CIRCLES-Comprehension Type

Home
Ask Doubt
Profile