Two circles are drawn through the points (a,5a)and(4a,a) to touch the y-axis. Prove that they intersect at angle tan−1(409).
tan−1(4/3)
tan−1(40/9)
tan−1(84/187)
π/4
The correct Answer is:B
Equation of any circle through the given points is:
(x−a)(x−4a)+(y−5a)(y−a)+λ(4x+3y−19a)=0, for some λ∈R.
As it touches the y-axis, putting x=0 and comparing discriminant of resulting quadratic equation in x to 0, we get
∴(−3a+3λ2)2=9a2−19λa
∴λ=0,−40a9.
∴ The required circles are
x2+y2−5ax−6ay+9a2=0
x2+y2−5ax−6ay+9a2−40a9(4x+3y−19a)=0
Hence centres are (5a2,3a) and (205a18,29a3)
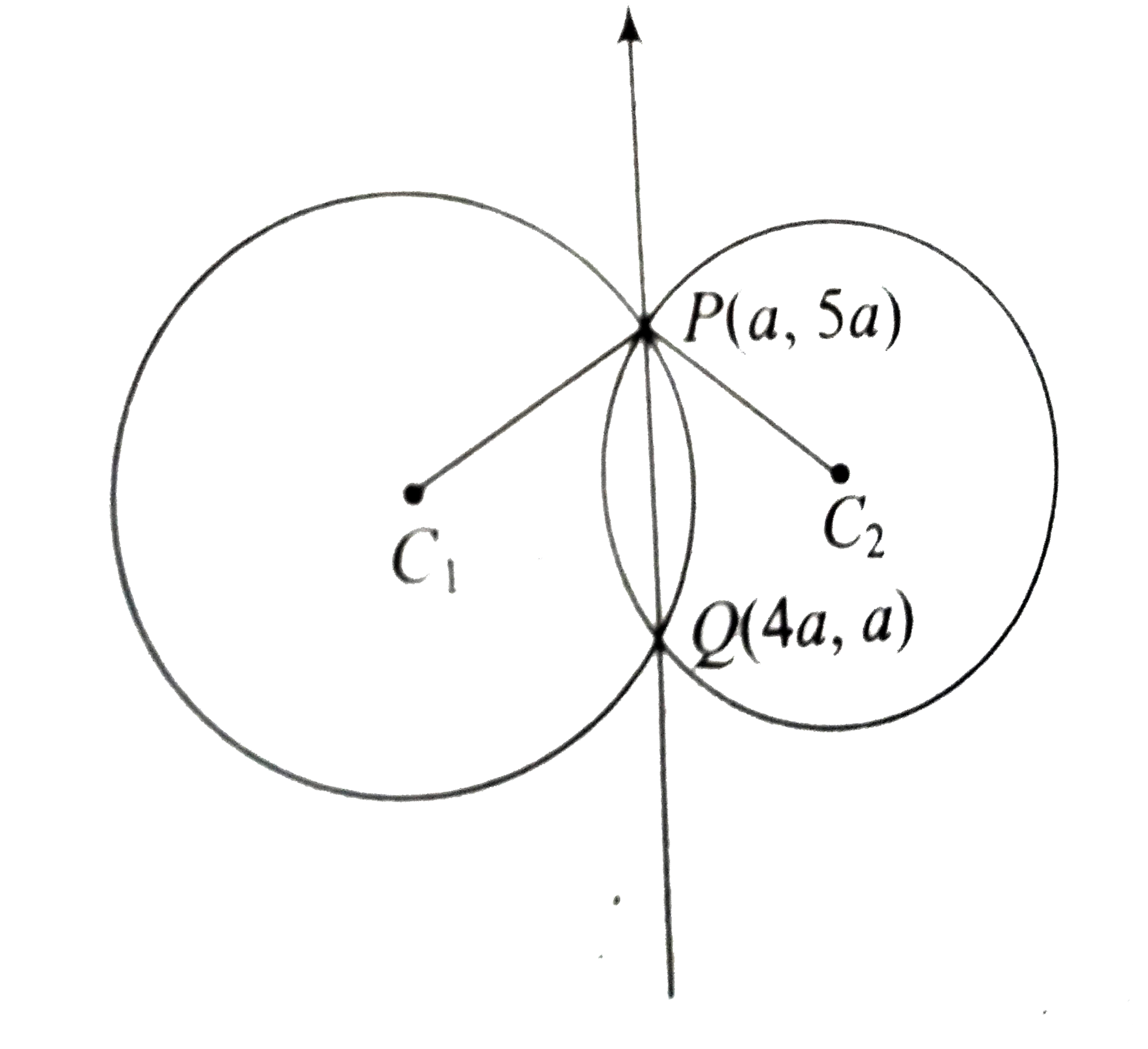
The centres of the given circles are:
C1(205a18,29a3) and C2(5a2,3a)
Now, the angle of intersection θ of these two circles is the angle between the radius vectors a the common point P to the two circles.
i.e., ∠C1PC2=θ
and slope of C2P=5a−3aa−5a2=−43
So, tanθ=84187+431−84187×43=252+748561−336=409
⇒θ=tan−1(409)
Topper's Solved these Questions
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Single Correct Answer Type
58 Videos
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank
32 Videos
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank
32 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - JEE Advanced (Single Correct Answer Type)
14 Videos
- COMPLEX NUMBERSBOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - Question Bank
30 Videos
Similar Questions
Knowledge Check
Equation of circle passing through the points (4, 3) and (2,5) and touching the axis of y is
Ax2+y2−20x−22y+121=0Bx2+y2−4x−6y+9=0Cx2+y2−10x−6y+13=0Dx2+y2+4x+6y+9=0Equations of circles which pass through the points (1,-2) and (3,-4) and touch the x-axis is
Ax2+y2+6x+2y+9=0Bx2+y2+10x+20y+25=0Cx2+y2−6x+4y+9=0DnoneThe circles which can be drawn to pass through (3,0) and (5,0) and to touch the y-axis intersect at an angle θ , then cosθ is equal to
A7/8B1/2C0Dnone of these
Find the equation of circle passing through the points (1,-2) and (3,-4) and touches the X-axis.
View SolutionThe circle which can be drawn to pass through (1, 0) and (3, 0) and to touch the y-axis intersect at angle θ. Then cosθ is equal to (a)12 (b) −12 (c) 14 (d) −14
View SolutionA circle passes through the points (2, 2) and (9, 9) and touches the x-axis. The absolute value of the difference of possible x-coordinate of the point of contact is______.
View Solutionthe equation of the circle passing through the point (2,1) and touching y-axis at the origin is
View SolutionFind the equation of the circle passing through the points A(4,3).B(2,5) and touching the axis of y. Also find the point P on the y-axis such that the angle APB has largest magnitude.
View Solution
