Transverse common tangents are drawn from O to the two circles C1,C2 with 4, 2 respectively. Then the ratio of the areas of triangles formed by the tangents drawn from O to the circles C1andC2 and chord of contacts of O w.r.t the circles C1andC2 respectively is
3 units
6 units
4 units
5 units
The correct Answer is:C
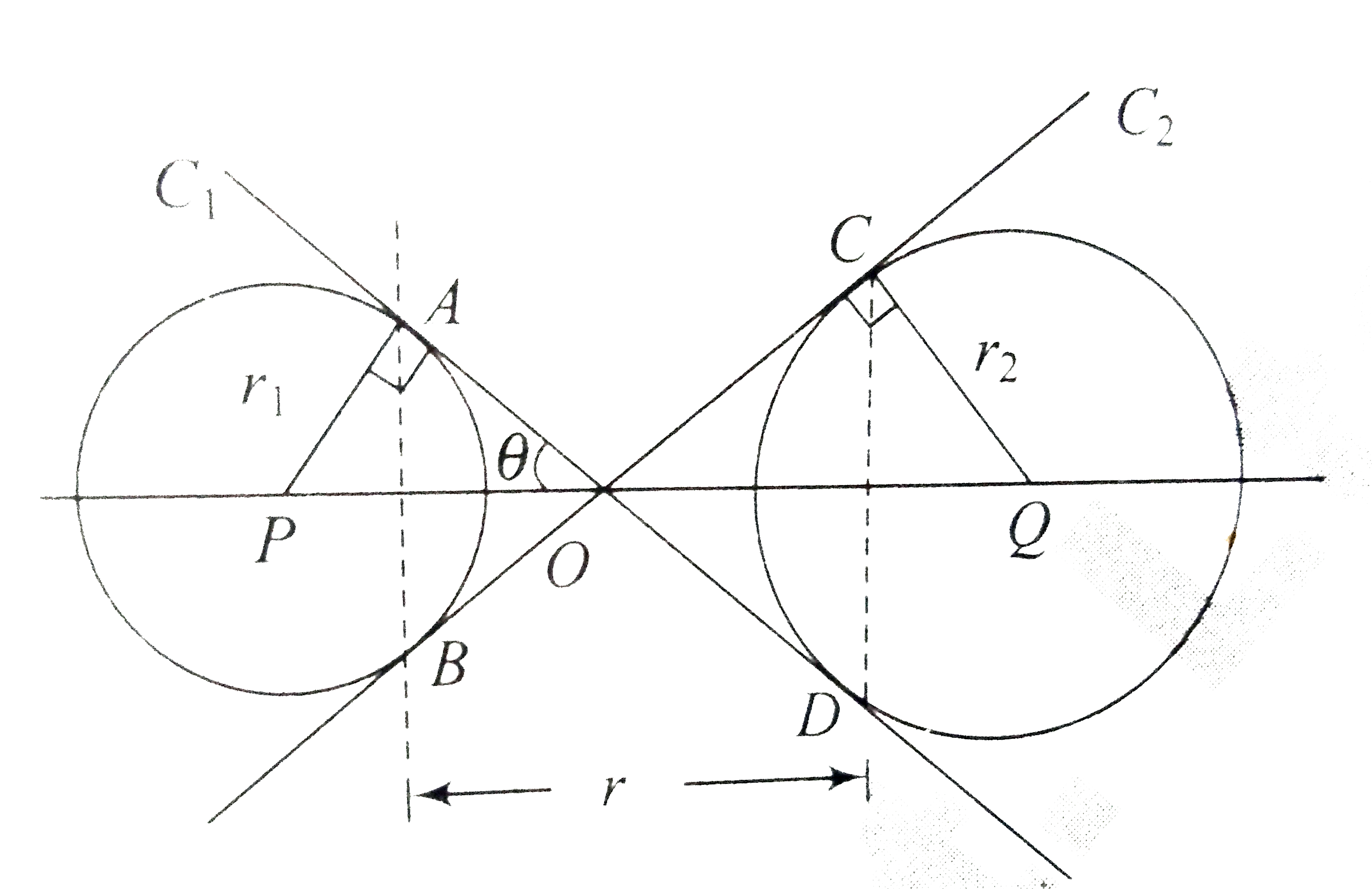
Let r1=2 and r2=4
Now, OPOQ=r1r2
OP=rr1r1+r2
OQ=rr1r1+r2
As triangles OAB and OCD are similar, we have
ar(ΔOCD)ar(ΔOAB)=(OC)2(OA)2=⎛⎜⎝rr2r2+r2sinθrr1r1+r2sinθ⎞⎟⎠=r21r21=4
Topper's Solved these Questions
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank
32 Videos
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Comprehension Type
8 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - JEE Advanced (Single Correct Answer Type)
14 Videos
- COMPLEX NUMBERSBOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - Question Bank
30 Videos
Similar Questions
Let the midpoint of the chord of contact of tangents drawn from A to the circle x2+y2=4 be M(1,−1) and the points of contact be B and C

View SolutionFor the circle x2+y2=r2, find the value of r for which the area enclosed by the tangents drawn from the point P(6,8) to the circle and the chord of contact and the chord of contact is maximum.
View Solution
Knowledge Check
If a chord of contact of tangents drawn from a point P with respect to the circle x2+y2=9 is x=2, then area, in square units, of triangle formed by tangents drawn from P to the circle and their chord of contact is equal to
A4√52B9√32C5√5)2Dnone of theseTangents OP and OQ are drawn from the origin O to the circle x2+y2+2gx+2fy+c=0. Then the equation of the circumcircle of the triangle OPQ is :
Ax2+y2+2gx+2fy=0Bx2+y2+gx+fy=0Cx2+y2−gx−fx=0Dx2+y2−2gx−2fy=0T is a point on the common tangents at P of two circles and if TA and TB are respectively the other tangents at A and B to the two circles drawn from the point T then
ATA=2TBBTA=TBCTA=12TBD3TA=TB
From a pt A common tangents are drawn to a circle x2+y2=a22andy2=4ax. Find the area of the quadrilateral formed by common tangents, chord of contact of circle and chord of contact of parabola.
View SolutionThe lengths of the tangents from A(-3,5) and B(1,2) to a circle are 6 and 5 respectively.Then the length of the tangent from C(5,-1) to the same circle is
View SolutionTangents are drawn from external poinl P(6,8) to the circle x2+y2=r2 find the radius r of the circle such that area of triangle formed by the tangents and chord of contact is maximum is (A) 25 (B) 15 (C) 5 (D) none
View SolutionTangents are drawn from the point (-1, 2) to the parabola y2=4x The area of the triangle for tangents and their chord of contact is
View SolutionArea of the triangle formed by tangents and chord of contact of the circle x2+y2+6x+8y=0 if tangents are drawn from the point "(1,1)" is
View Solution