A circle of radius 2 has its centre at (2, 0) and another circle of radius 1 has its centre at (5, 0). A line is tangent to the two circles at point in the first quadrant. The y-intercept of the tangent line is
√2
2√2
3√2
4√2
The correct Answer is:B
12=a−5a−2⇒a=8
Thus, equation of line is y=m(x−8)
Now, this line touches the circle.
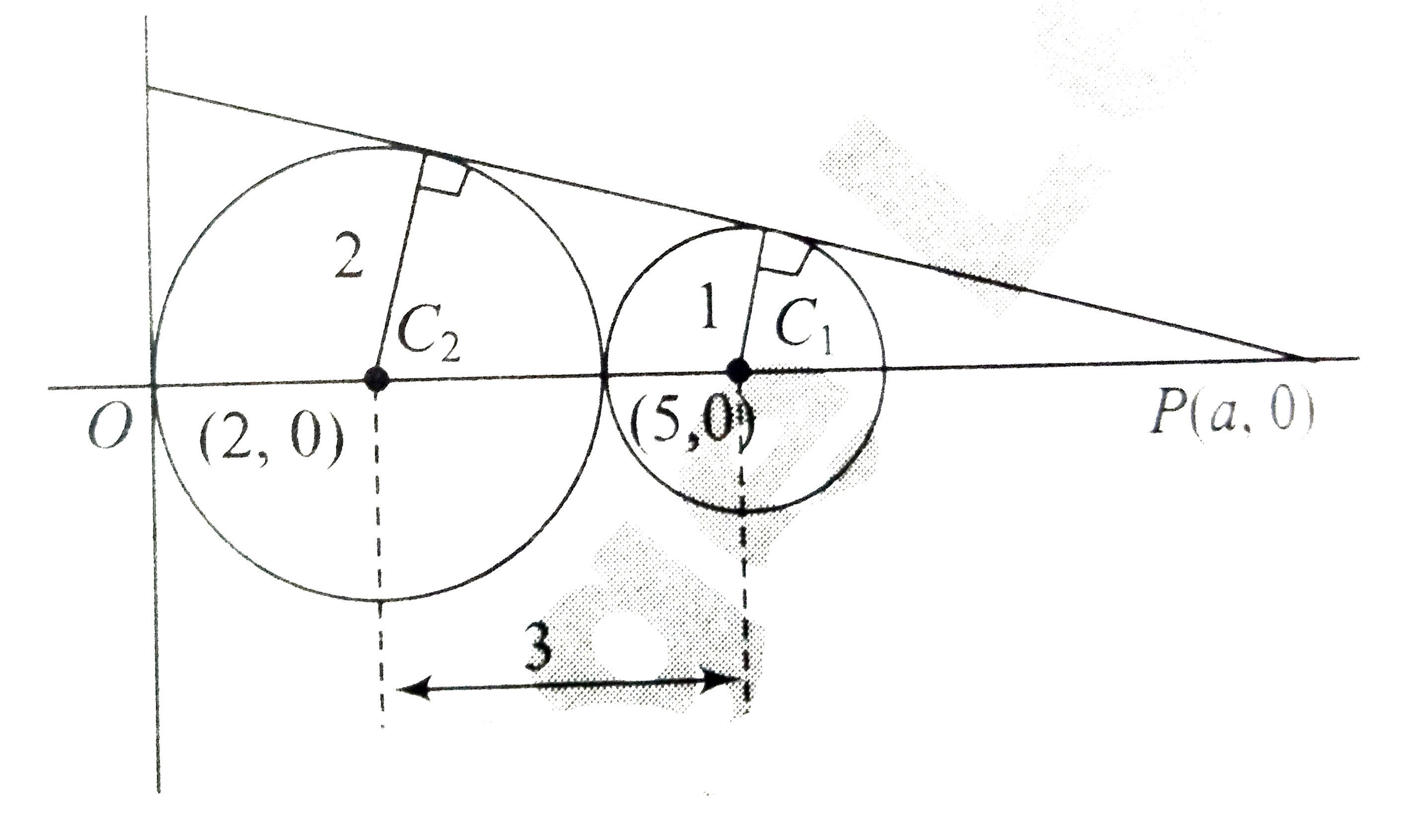
∴∣∣∣6m√1+m2∣∣∣=2
⇒9m2=1+m2
∴m=−1√8
⇒ y-intercept =√8=2√2.
Topper's Solved these Questions
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank
32 Videos
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Comprehension Type
8 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - JEE Advanced (Single Correct Answer Type)
14 Videos
- COMPLEX NUMBERSBOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - Question Bank
30 Videos
Similar Questions
Knowledge Check
A line touches a circle of radius 6 cm. Another line is drawn which is tangent to the circle. If the two lines are parallel, then the distance between them is:
A6 cmB12 cmC8 cmD10 cmIf 3x+y=0 is a tangent to a circle whose center is (2,−1) , then find the equation of the other tangent to the circle from the origin.
Ax−3y=0Bx+3y=0C3x−y=0Dx+2y=0A point P is 13 xm from the centre of a circle . Radius of the circle is 5 cm . A tangent is drawn from point P to the circle , then the length of the tangent is :
A10B11C12D13
One circle has a radius of 5 and its centre at (0,5). A second circle has a radius of 12and its centre at (12,0). What is the length of a radius of a third circle which passes through the centre of the second circle and both the points of intersection of the first two circles.
View SolutionA circle of radius 5 has its centre on the negative x-axis and passes through the point (2,3). The intercept made by the circle on the y-axis is
View SolutionThe line y=x is a tangent at (0,0) to a circle of radius unity. The center of the circle is
View SolutionDraw a circle of radius 3 cm. From a point 5 cm from the centre of the circle, draw two tangents to the circle. Measure the length of each tangent.
View Solution3x+4y−7=0 is common tangent at (1, 1) to two equal circles of radius 5. Their centres are the points
View Solution
