Question

Draw the graph of $y={\sin }^{2}x-\cos x$

Explanation

Clearly, the domain of the function is R.
Also `f(x)` is a periodic function is R.
Lets first draw the graph of `y=f(x)` for `0 le x le 2pi`.
`f(0) =0-1=-1`
`f(x)=0 therefore sin^(2)x - cosx=0`
or `cos^(2)x +cosx-1=0`
or `cosx=(-1+-sqrt(5))/(2)`
or `cosx = (-1+sqrt(5))/(2) (therefore cosx ne (-1-sqrt(5))/(2) (lt -1))`
Now, `f^(')(x)=0 therefore sin x(2cosx+1)=0`
`therefore x=pi` (considering `0 lt x lt 2pi)` or `x = (2pi//3), 4pi//3`
Now the sign scheme of `f^(')(x)` is as follows:

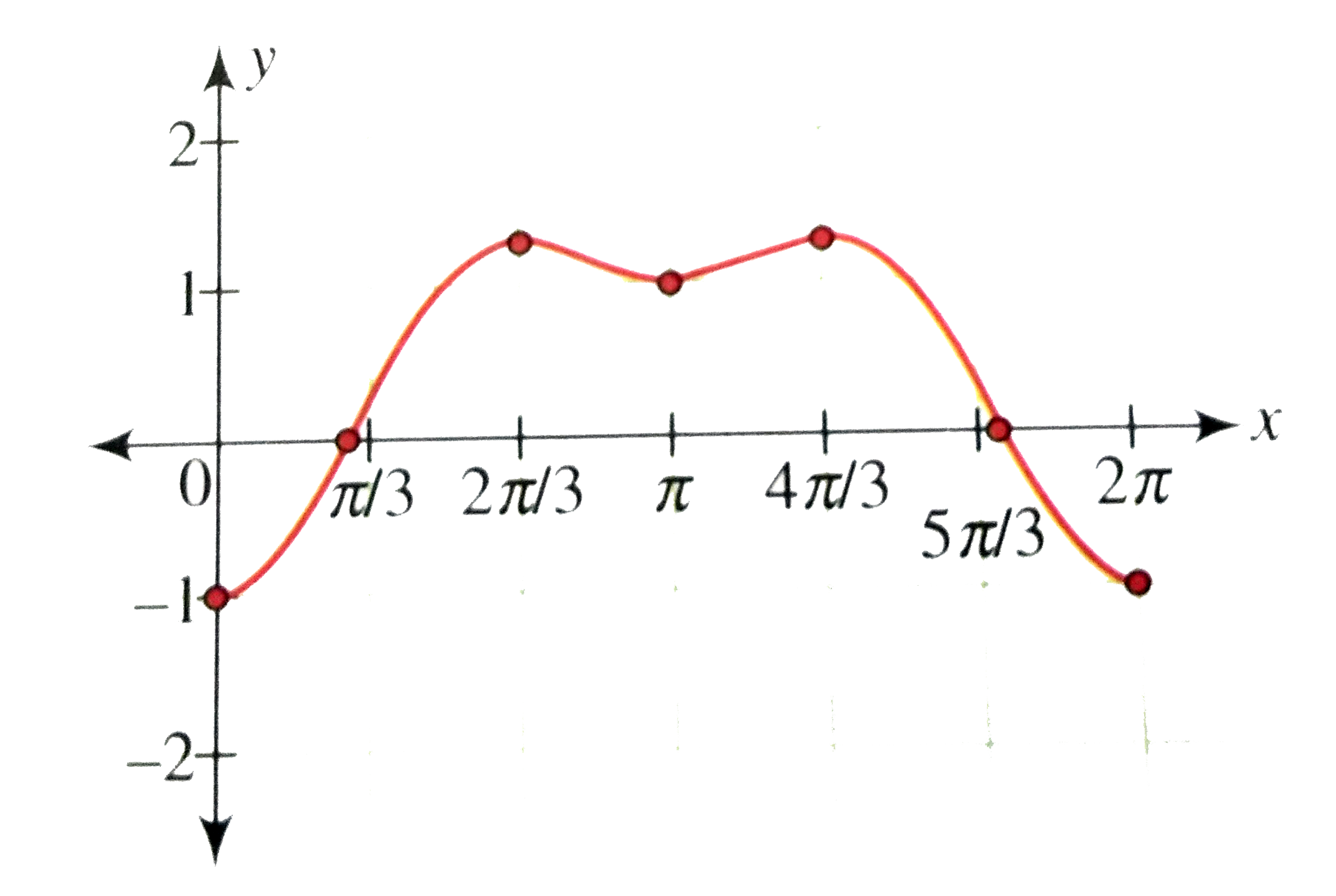
So `x=2pi//3, 4pi//3` are the points of maximum and `x = pi` is the point of minima.
`f(pi) = 1, f(2pi//3)=f(4pi//3)=3/4+1/2=5/4`
From the above discussion, we have the following important points on graph paper.

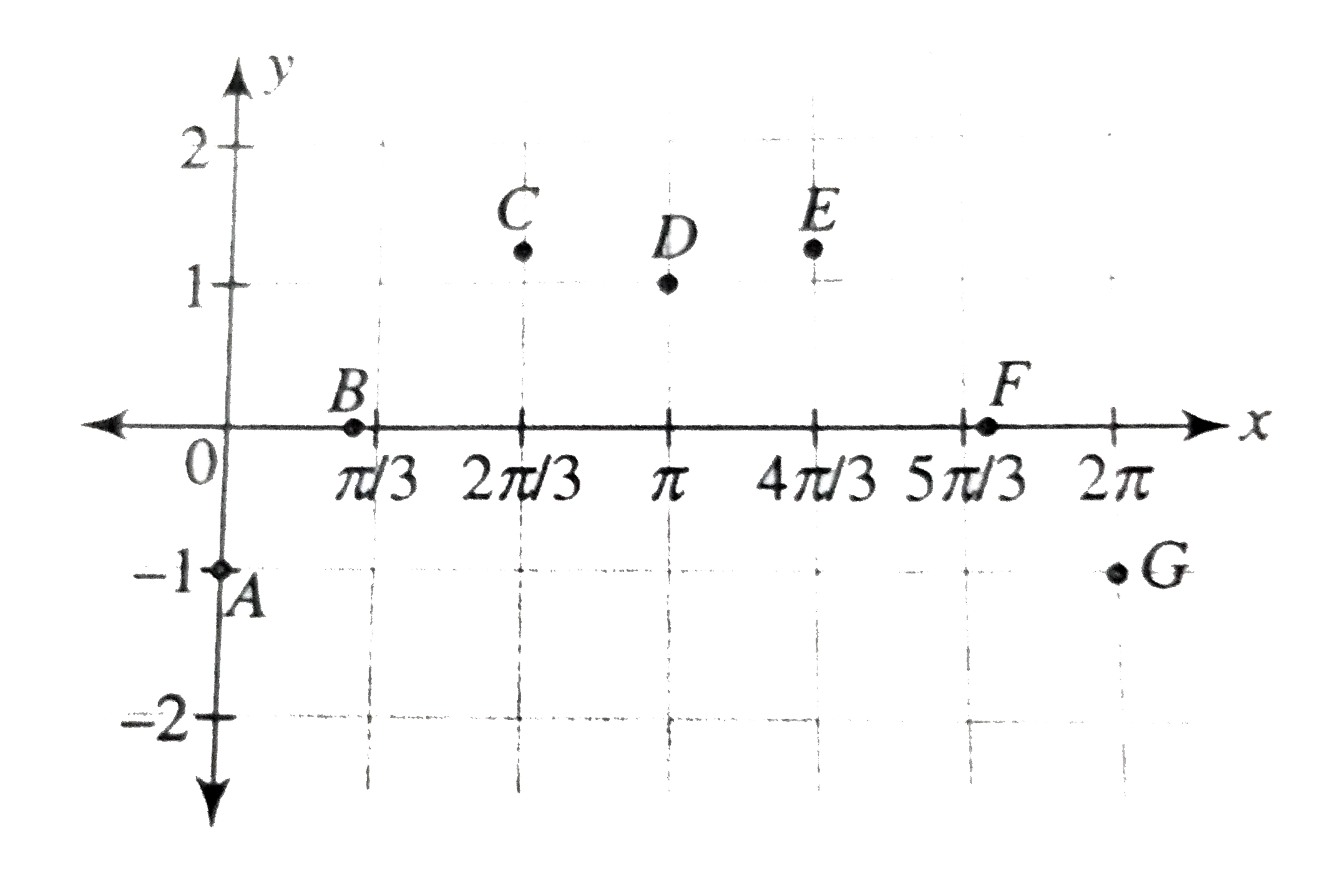
From points A to C, `f(x)` increases, from C to D, `f(x)` decreases, from D to E, `f(x)` increases, from E to G, `f(x)` decreases.
Hence, the graph of `y=f(x)` for `0 lt x lt 2pi` is as shown in the following figure.

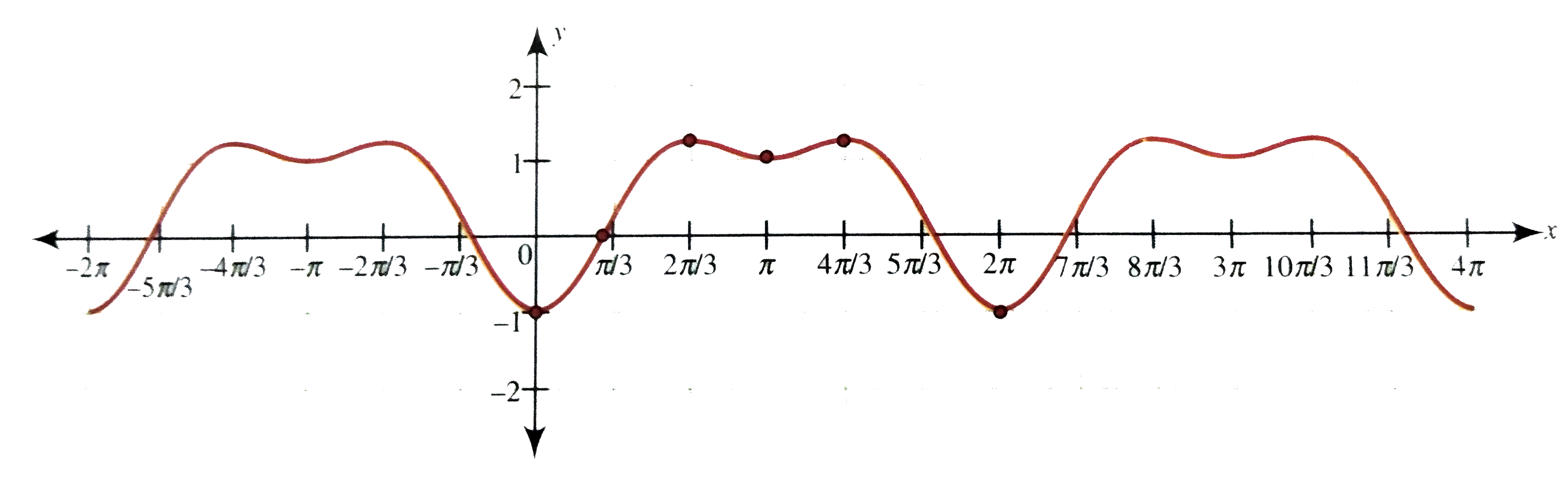
Now `f(x)` is periodic with period `2pi`, repeat the above graph for other intervals as shown in the following figure.