Draw the graph y=sin2x.
Video Solution
Text Solution
We have y=f(x)=sin2x
Clrearly, f(x+π)=f(x)
Hence y = f(x) has period π.
So first we draw the graph for x∈[0,π].
f(0)=f(π)=0 and f(π/2)=1
Hence the graphs of y = sin x and y=sin2x coincide for x = 0, π/2 and π.
For x∈(0,π/2)∪(π/2,π),sinx∈(0,1)
∴sin2x<sinx
So the graph of y=sin2x lies below the graph of y = sin x.
So the graphs of both the functions are as shown in the following figure.
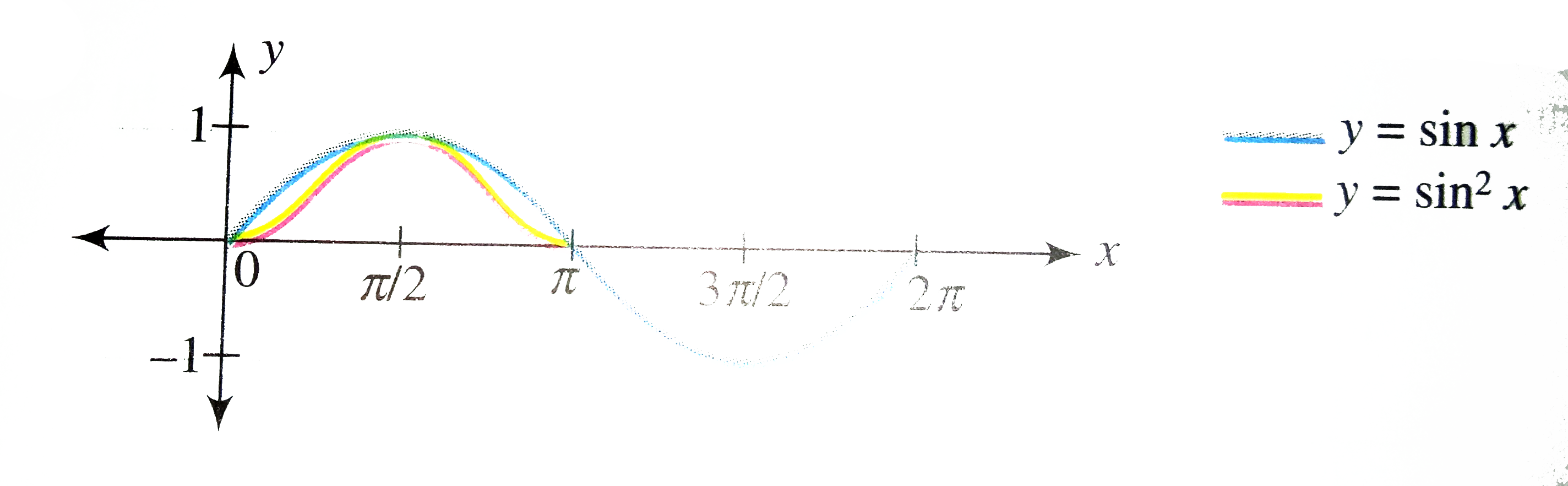
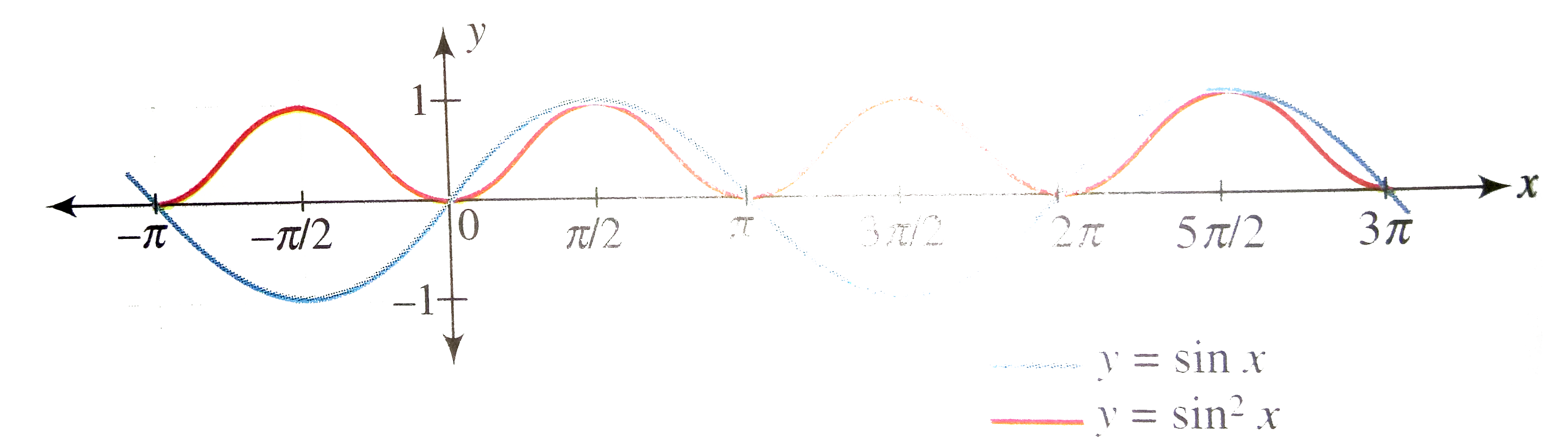
Since the period of the function is π, the graph is repeated as shown in the following figure.
|
Topper's Solved these Questions
- GRAPHS OF TRIGONOMETRIC FUNCTIONSBook:CENGAGEChapter:GRAPHS OF TRIGONOMETRIC FUNCTIONSExercise:Exercise
Explore 22 Videos
- GRAPHS OF ELEMENTARY FUNCTIONS Book:CENGAGEChapter:GRAPHS OF ELEMENTARY FUNCTIONS Exercise:Exercise
Explore 34 Videos
- HIGHT AND DISTANCE Book:CENGAGEChapter:HIGHT AND DISTANCE Exercise:JEE Previous Year
Explore 3 Videos
Similar Questions
Draw the graph of y=sin3x.
View SolutionDraw the graph of y=sin2x−cosx
View SolutionDraw the graph of y=sin2x.
View SolutionDraw the graph of y=3sin2x.
View SolutionDraw the graph of y=cos2x.
View SolutionDraw the graph of y=sin−1(x2)
View SolutionDraw the graph of y = x sin x.
View SolutionDraw the graph of y=sin−1(x−3).
View SolutionDraw the graph of y=sin−1|x|.
View SolutionDraw the graph of y=sin−1x3 and compare wire the graph of y=sin−1x.
View Solution