For f(x)=sinx−x2+1, check weather the function is increasing, decreasing or has a point of extremum ?
f(x)=sinx−x2+1
∴ f'(x)=cosx−2x
Now draw the graphs of y = cos x and y = 2x.
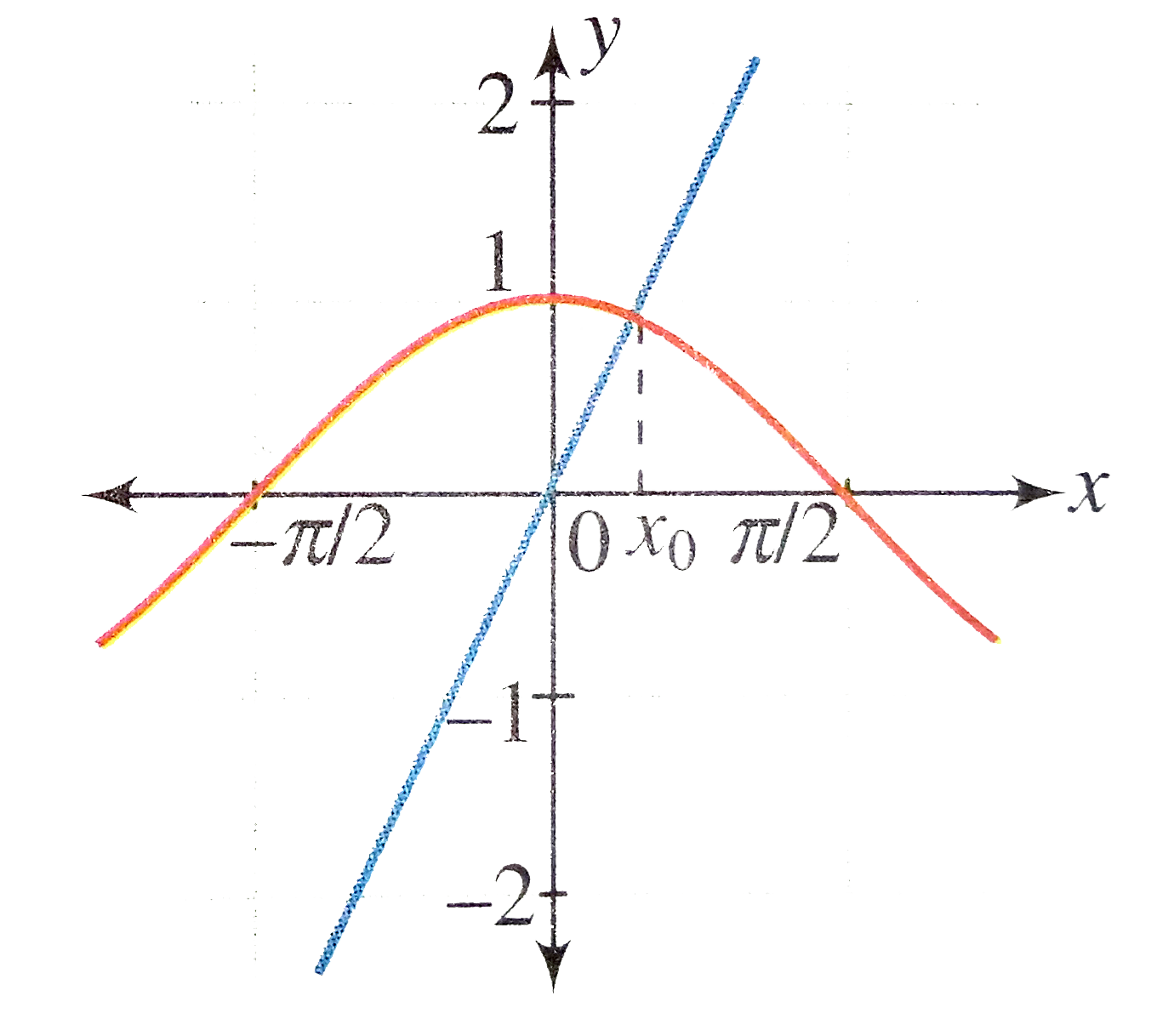
From the graph, for x<x0,cosx>2x⇒f'(x)>0
x>x0,cosx<2x⇒f'(x)<0
Hence x=x0 is the point of maxima.
Topper's Solved these Questions
- GRAPHS OF TRIGONOMETRIC FUNCTIONSBOOK - CENGAGECHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise
22 Videos
- GRAPHS OF ELEMENTARY FUNCTIONS BOOK - CENGAGECHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - Exercise
34 Videos
- HIGHT AND DISTANCE BOOK - CENGAGECHAPTER - HIGHT AND DISTANCE EXERCISE - JEE Previous Year
3 Videos
Similar Questions
the function f(x)=x2−x+1 is increasing and decreasing
View SolutionLet f''(x)>0 and ϕ(x)=f(x)+f(2−x),x∈(0,2) be a function then the function ϕ(x) is (A) increasing in (0,1) and decreasing (1,2) (B) decreasing in (0, 1) and increasing (1,2) (C) increasing in (0, 2) (D) decreasing in (0,2)
View Solution
Knowledge Check
which of the folloiwng function has point of extremum at x =0?
Af(x) =e−|x|Bf(x) = sin |x|Cf(x)={x2+4x+3x<0−xx≥0Df(x)={x2+4x+3x<0−xx≥0The function f(x)=x4−2x3+1 is decreasing for
Ax≥32Bx>32Cx≤32Dx<32The function f(x)=xx2+1 decreasing, if
Ax<−1andx>1B−1<x<1Cx<−1 or x>1Dx≤1andx≥1
Prove that the function f(x)=x2−x+1 is neither increasing nor decreasing on (−1, 1) .
View SolutionFind the interval of increasing and decreasing of the function f(x)=logxx
View SolutionWhich of the following statement is always true? (a)If f(x) is increasing, the f−1(x) is decreasing. (b)If f(x) is increasing, then 1f(x) is also increasing. (c)If fandg are positive functions and f is increasing and g is decreasing, then fg is a decreasing function. (d)If fandg are positive functions and f is decreasing and g is increasing, the fg is a decreasing function.
View SolutionThe function f(x)=x3−3x2+3x−100 ,for all real values of x is
O increasing
O decreasing
O increasing & decreasing
O Neither increasing nor decreasing
View SolutionWhat is the value of p for which the function f(x)=psinx+(sin 3x)/xhasanextreμmatx=pi/3 ?
View Solution
