Question

The number of solutions of $\tan x-mx=0,m>1,$
in $(-\frac{\pi }{2},\frac{\pi }{2})$
is
1 (b) 2
(c) 3 (d)
$m$

Explanation

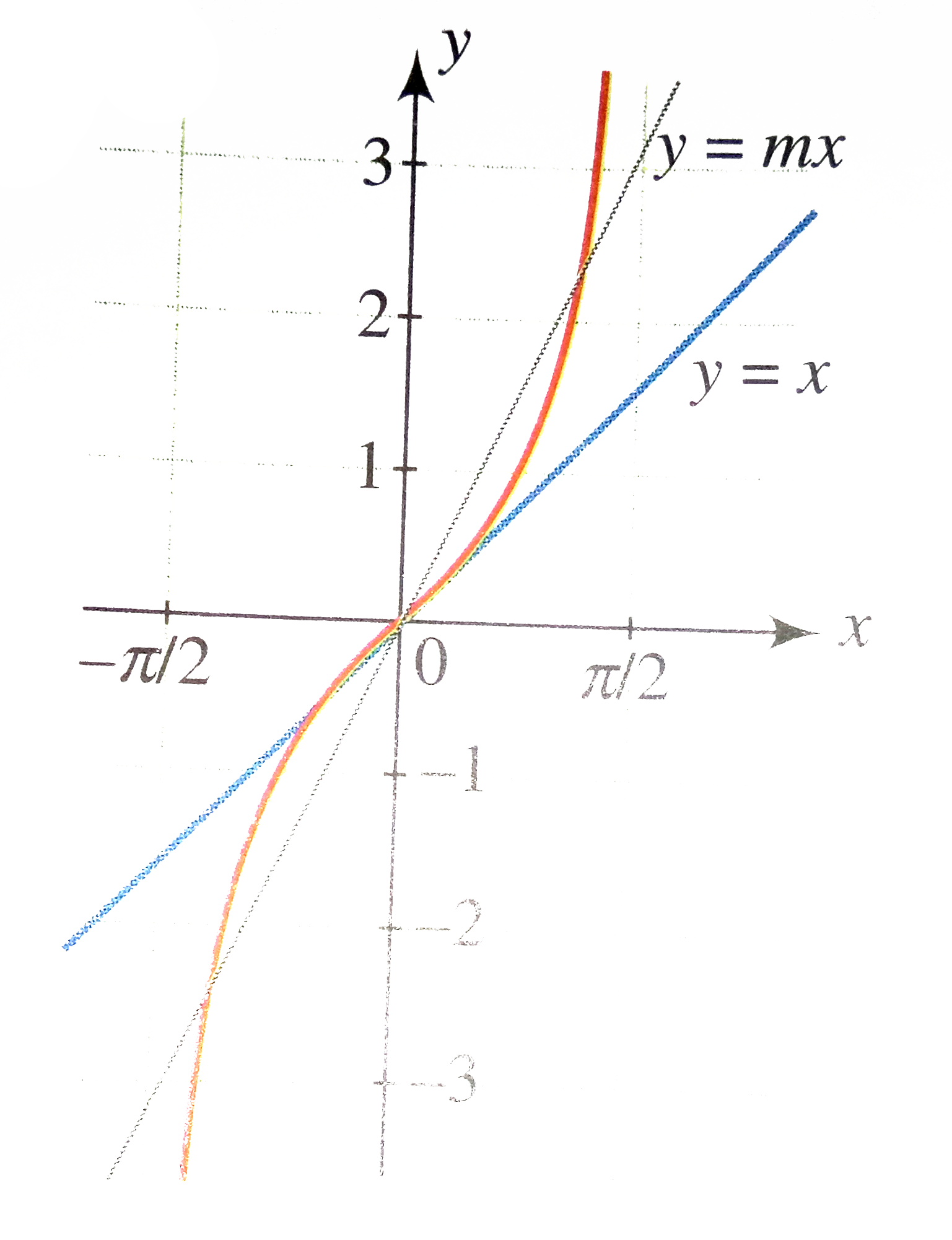
In `(-(pi)/(2), 0)`, the graph of y = tan x lies below the line y = x, which is the tangent at x = 0 and in `(0, (pi)/(2))`, it lies above the line y = x.
For `m gt 1`, the line y = mx lies below y = x in `(-(pi)/(2), 0)` and above y = x in `(0, (pi)/(2))`. The graphs of y = tan x and y = mx, `m gt 1`, meet at three points,
including x = 0 in `(- (pi)/(2), (pi)/(2))`.