Draw the graph of y=√1+x2−x
Video Solution
Text Solution
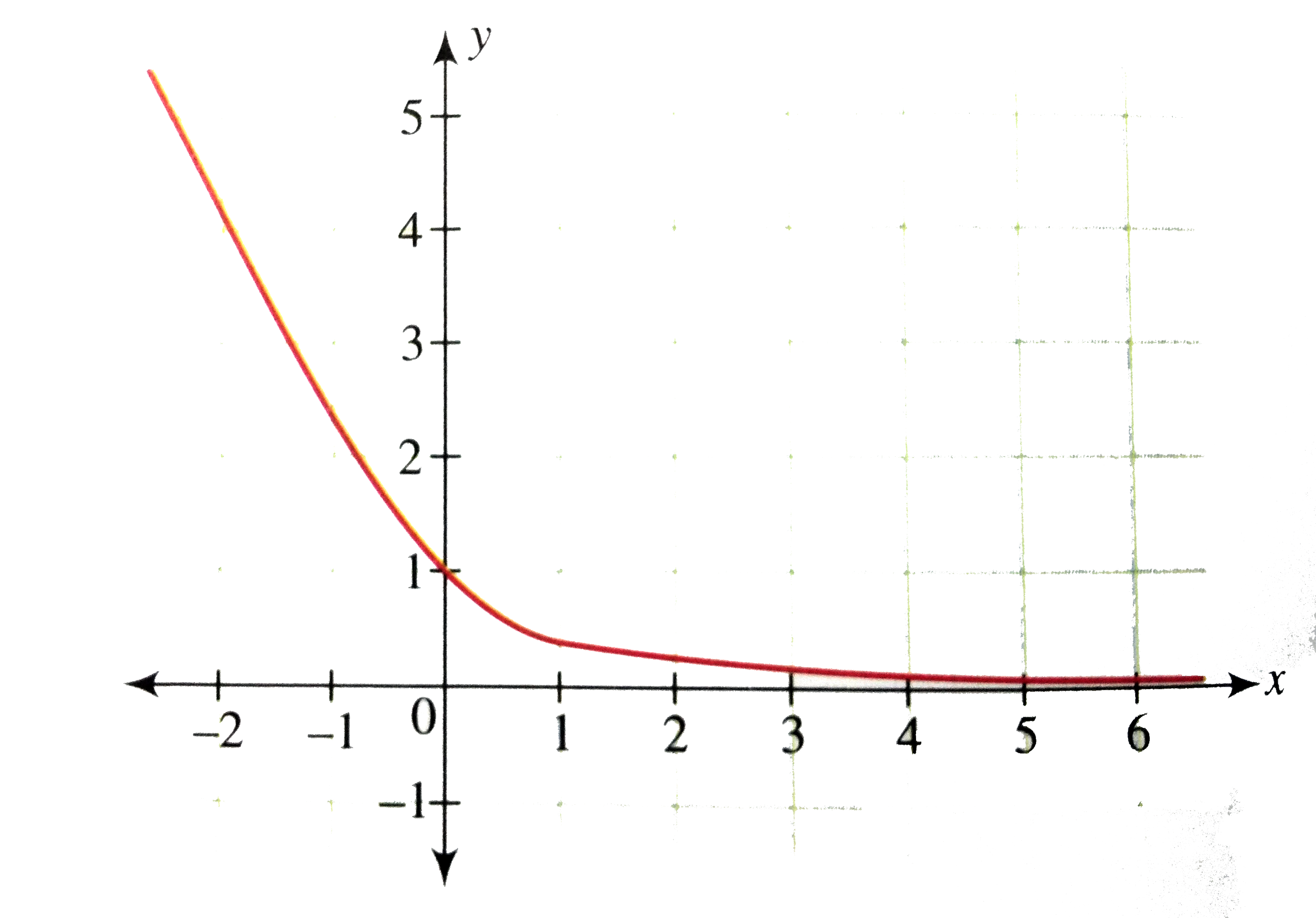
We have y=f(x)=√1−x2−x
Clearly, the domain of function is R.
f(0)=1
f(x)=0∴1+x2=x2, which is not possible.
Therefore, the function never intersect the x-axis.
Also, √1+x2>x,∀x∈R
graph of y=f(x) always lies above the x-axis.
limx→∞(√1+x2−x)=limx→∞1√1+x2+x=0
limx→∞(√1+x2−x)=∞
f′(x)=1√1+x2−1=(1−√1+x2√1+x2<0),∀x∈R
Hence, the function is always decreasing.
From the above information, the graph of the function is as shown in the figure.
|
Topper's Solved these Questions
Similar Questions
Draw the graph of y=√x2−1
View SolutionDraw the graph of y=−√x2+2
View SolutionDraw the graph of y=2x.
View SolutionDraw the graph of y=|x|
View SolutionDraw the graph of y=(√x2+1−√x2−1)
View SolutionDraw the graph of y=√xx−1
View SolutionDraw the graph of y=3√x2+1x−1
View SolutionDraw the graph of y=−√6−3x2
View SolutionDraw the graph of y=sin−1(x2)
View SolutionDraw the graph of y≤x+2.
View Solution
