Draw the graph of the relation $y^{2} = x^{5} (2 - x)$

Video Solution

Text Solution

Verified by Experts

We have $y^{2} = x^{5} (2 - x)$
$∴ y = \pm \sqrt{2 x - x^{2}}$
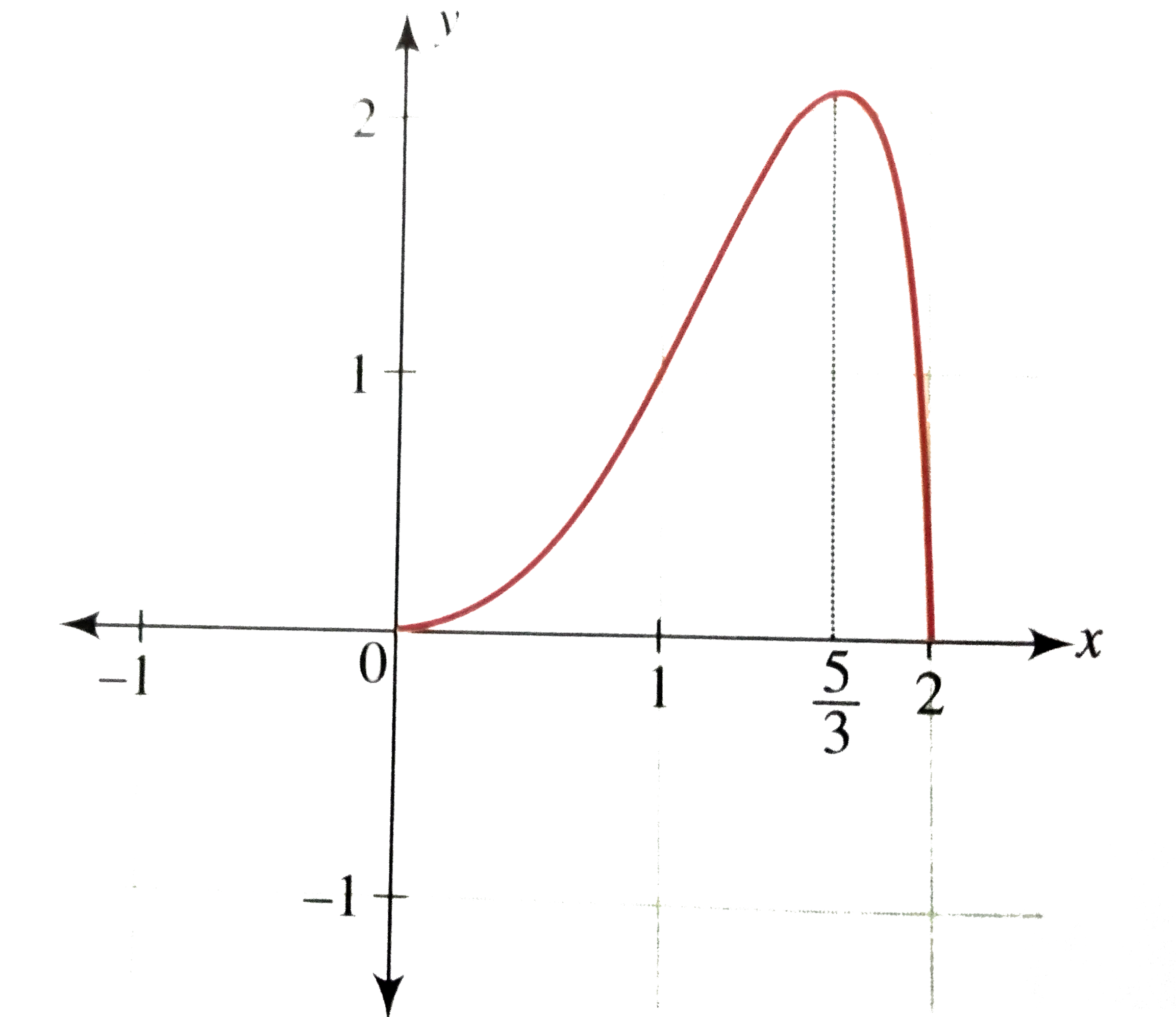
Let us first draw the graph of $y = f (x) = x^{2} \sqrt{2 x - x^{2}}$ .
Clearly, the domain of function is $[0, 2]$ .
So, the graph meets the x-axis at (0,0) and (2,0).
Also $f (x) \geq 0$
$f^{'} (x) = 2 x \sqrt{2 x - x^{2}} + x^{2} \frac{1 - x}{\sqrt{2 x - x^{2}}} = \frac{x^{2} (5 - 3 x)}{\sqrt{2 x - x^{2}}}$
$f^{'} (x) = 0$ $∴ x = 5 / 3$ , which is the point of maxima.
$f^{''} (x) = \frac{(10 x - 9 x^{2}) \sqrt{2 x - x^{2}} - \frac{1 - x}{\sqrt{2 x - x^{2}}} (5 x^{2} - 3 x^{2})}{2 x - x^{2}}$
$x^{2} \frac{6 x^{2} - 20 x + 15}{(2 x - x^{2} \sqrt{2 x - x^{2}})}$
$f^{''} (x) = 0 ∴ x = \frac{10 - \sqrt{10}}{6}$ , which is the point of inflection.
Hence, the graph of $y = f (x)$ is as shown in the following figure.

To draw the graph of $y = - x^{2} \sqrt{2 x - x^{2}}$ , reflect the above graph in the x-axis.
Hence, the graph of the given relation $y^{2} = x^{5} (2 - x)$ is as shown in the following figure.

|

Updated on:21/07/2023

Class 12 MATHS FUNDAMENTAL OF MATHEMATICS

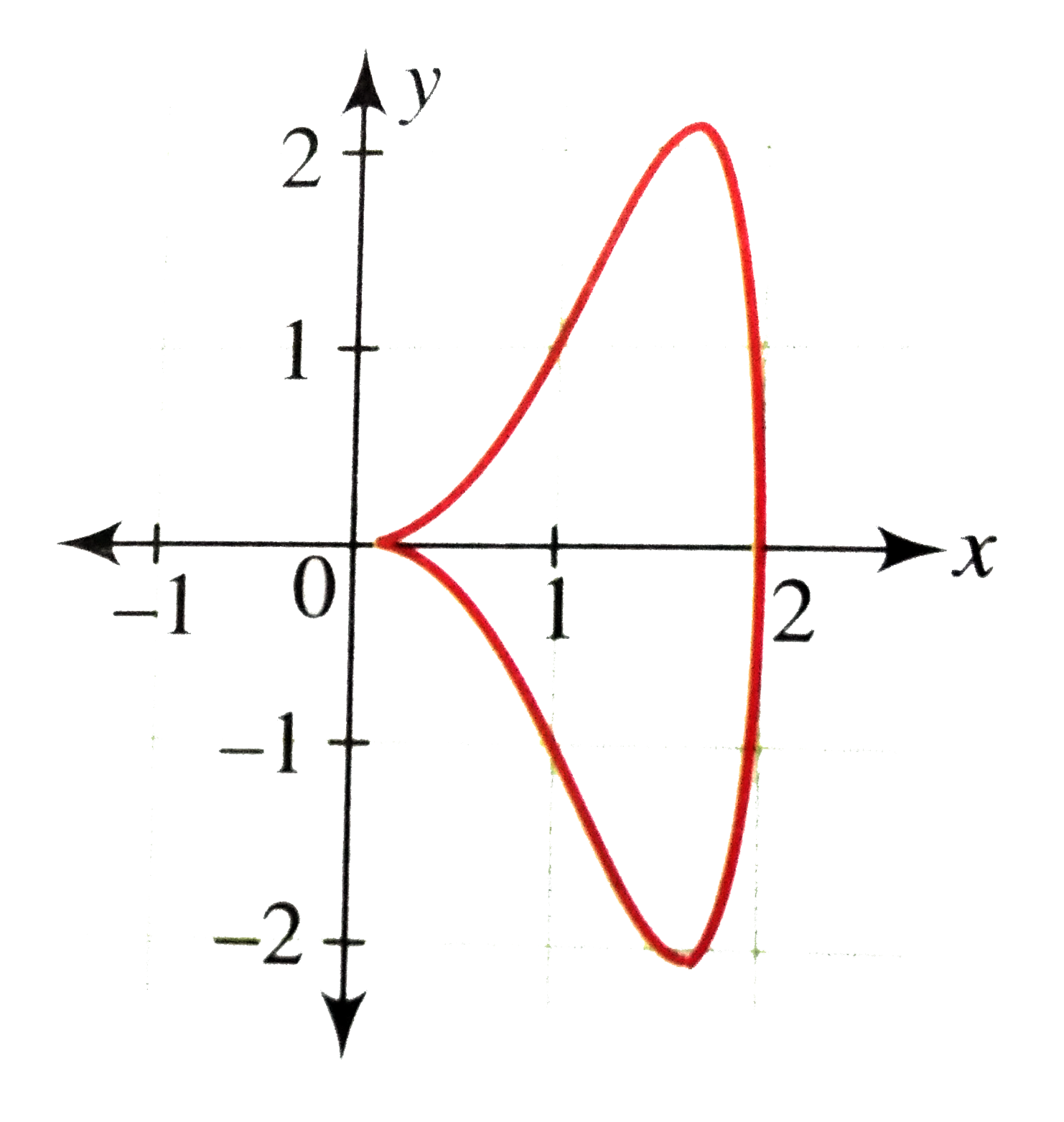
Topper's Solved these Questions

Similar Questions

CENGAGE-CURVE TRACING-Exercise

Home
Ask Doubt
Profile