The function f(x)=x13(x−1) has two inflection points has one point of extremum is non-differentiable has range [−3x2−83,∞)
Video Solution
Text Solution
y=x1/3(x−1)
dydx=43x1/3−13.1/x2/3=13x2/3[4x−1]
Hence f is increasing for x>14 and decreasing for x<14
Thus, x=1/4 is the point of minima.
f′(0) does not exist as f(x) is a vertical tangent here.
f''(x)=49.1x2/3+13.23.1x5/3
=29x2/3[2+1x]=29x2/3[2x+1x]
∴f''(x)=0 at x=−12
Thus, x=−12 is the point of inflection.
From the above discussion, the graph of function is as shown in the following figure.
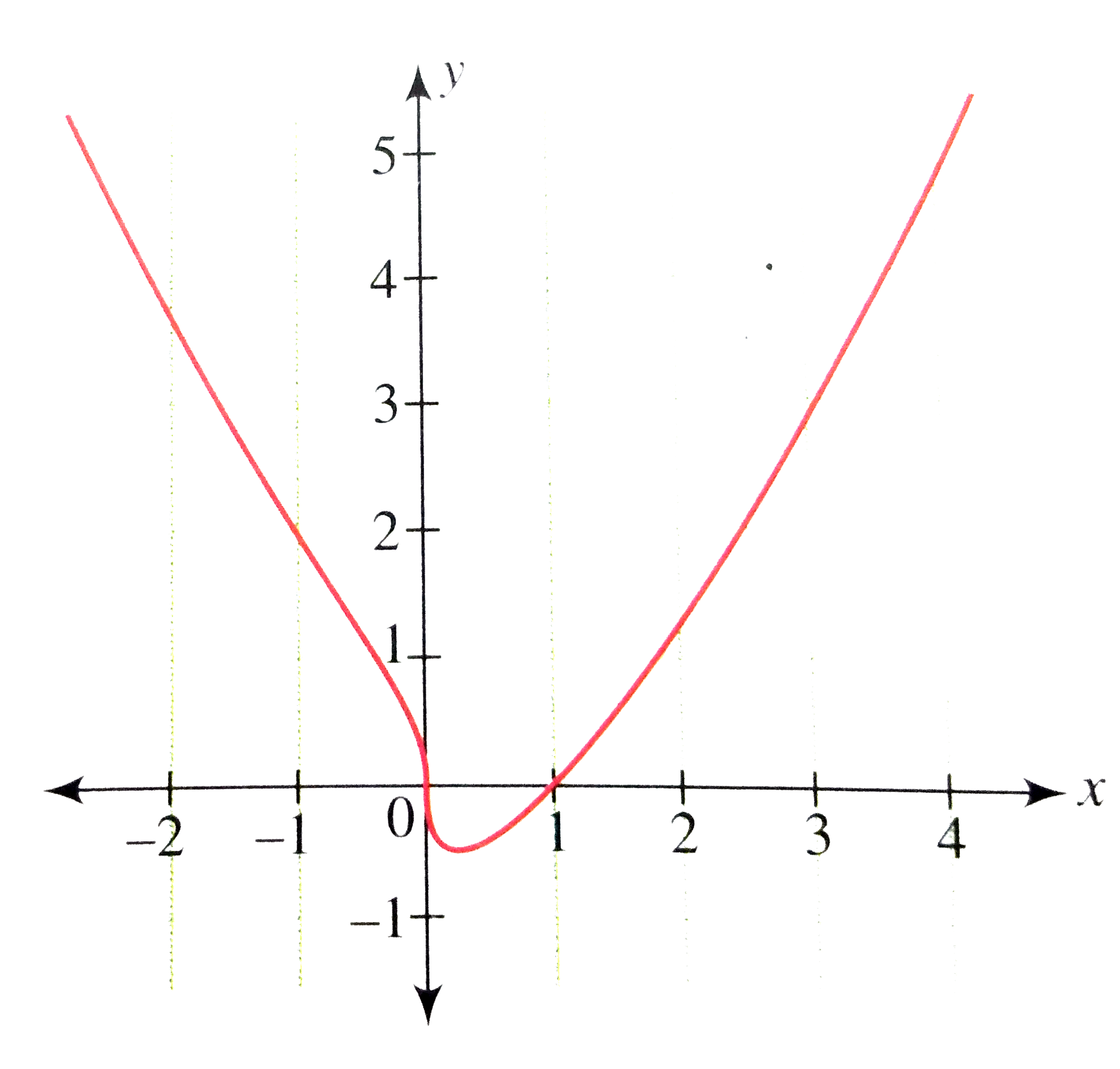
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
which of the folloiwng function has point of extremum at x =0?
Af(x) =e−|x|Bf(x) = sin |x|Cf(x)={x2+4x+3x<0−xx≥0Df(x)={x2+4x+3x<0−xx≥0f(x)=2x3+3x2−12x+7 has maximum at the point
A(1,0)B(2,9)C(−2,9)D(−2,27)
f(x)=x15 at x=0 has inflection point. y D.N.E. at x=0
View SolutionWhich of the following hold(s) good for the function f(x)=2x−3x23? (a)f(x) has two points of extremum. (b)f(x) is convave upward ∀x∈R. (c)f(x) is non-differentiable function. (d)f(x) is continuous function.
View Solutionf(x)=∣∣x2−1∣∣ has no inflection point in its domain as no tangent can be drawn at these points.
View SolutionLet f(x)=x3+3x(Inx−1) when x∈(0,∞) where f(x) has point of extremum at x=k. Then -
View SolutionIf the function f(x)=∣∣x2+a∣∣x|+b| has exactly three points of non-derivability, then
View SolutionThe number of points of extremum of the function f(x)=(x−2)23(2x+1) is
View Solution