Draw the graph of y=sinxcos2x
Video Solution
Text Solution
We have y=f(x)=sinxcos2x
Clearly, the domain of f(x) is R.
Also the period of f(x) is R.
Let us first draw the graph of y=f(x) for 0≤x≤2π
f(x)=0∴sinx=0 or cos2x=0
∴x=0,π,2π or x=π/2,3π/2
f(x)>0, for x∈(0,π) and f(x)<0, for x∈(π,2π)
Now f′(x)=cosxcos2x+sinx(−2sinxcosx)
=cosx(cos2x−2sin2x)
f′(x)=0∴cosx=0 or tan2x=1/2
∴x=π2,3π2 or x=tan−11√2,π−tan−11√2,π+tan−11√2,2π−tan−11√2
Now we can draw the graph of y=f(x) for x∈(0,π)
For x∈(π,2π), we reflect the graph of y=f(x) for x∈(0,π) in the x-axis as f(π−x)=−f(π+x)
f(tan−11√2)=f(π−tan−11√2)=23√3
From the above discussion, we have, following important points on graph paper.
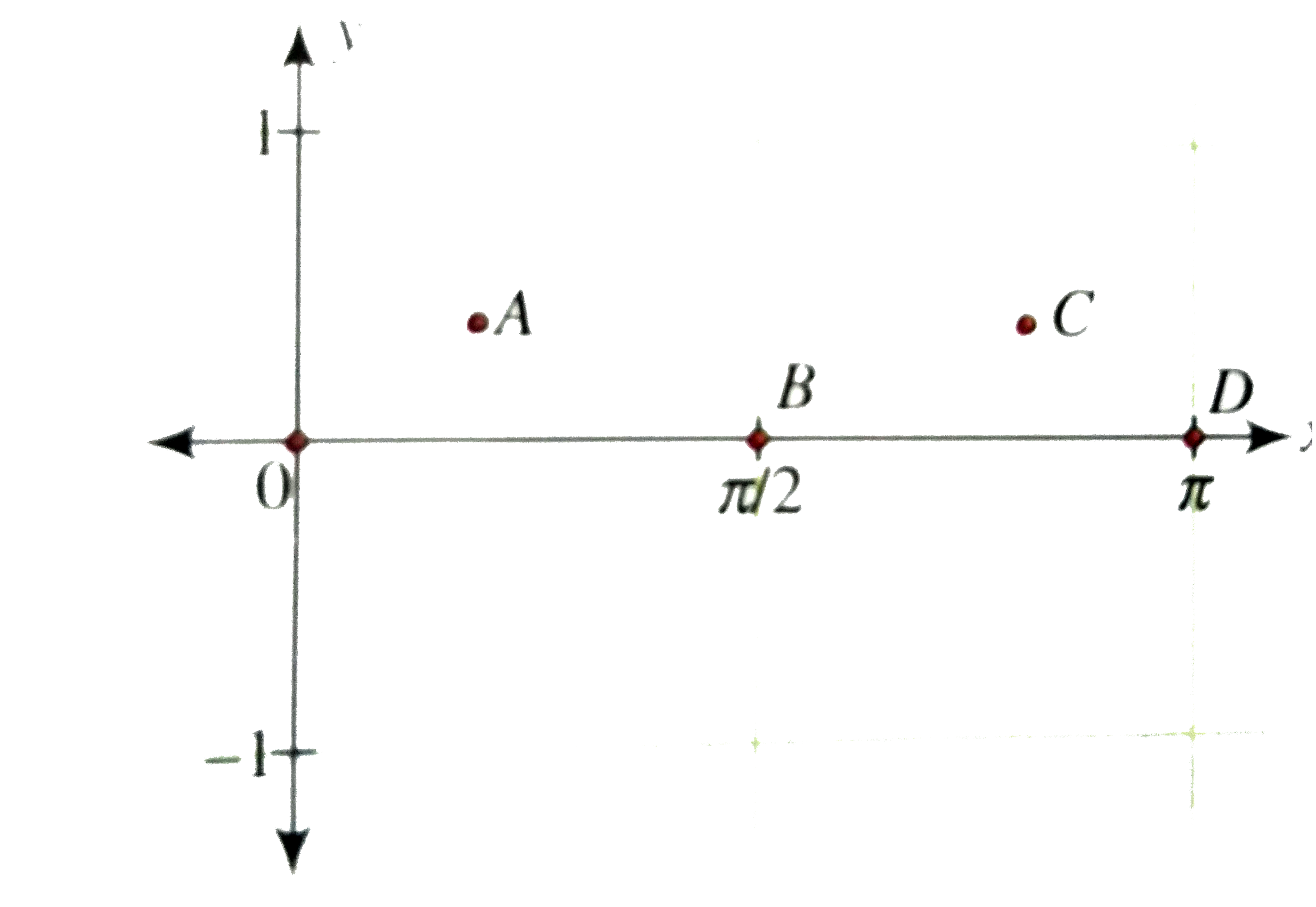
f(x) increases from O to A, decreases from A to B, increases from B to C, decreases from C to D.
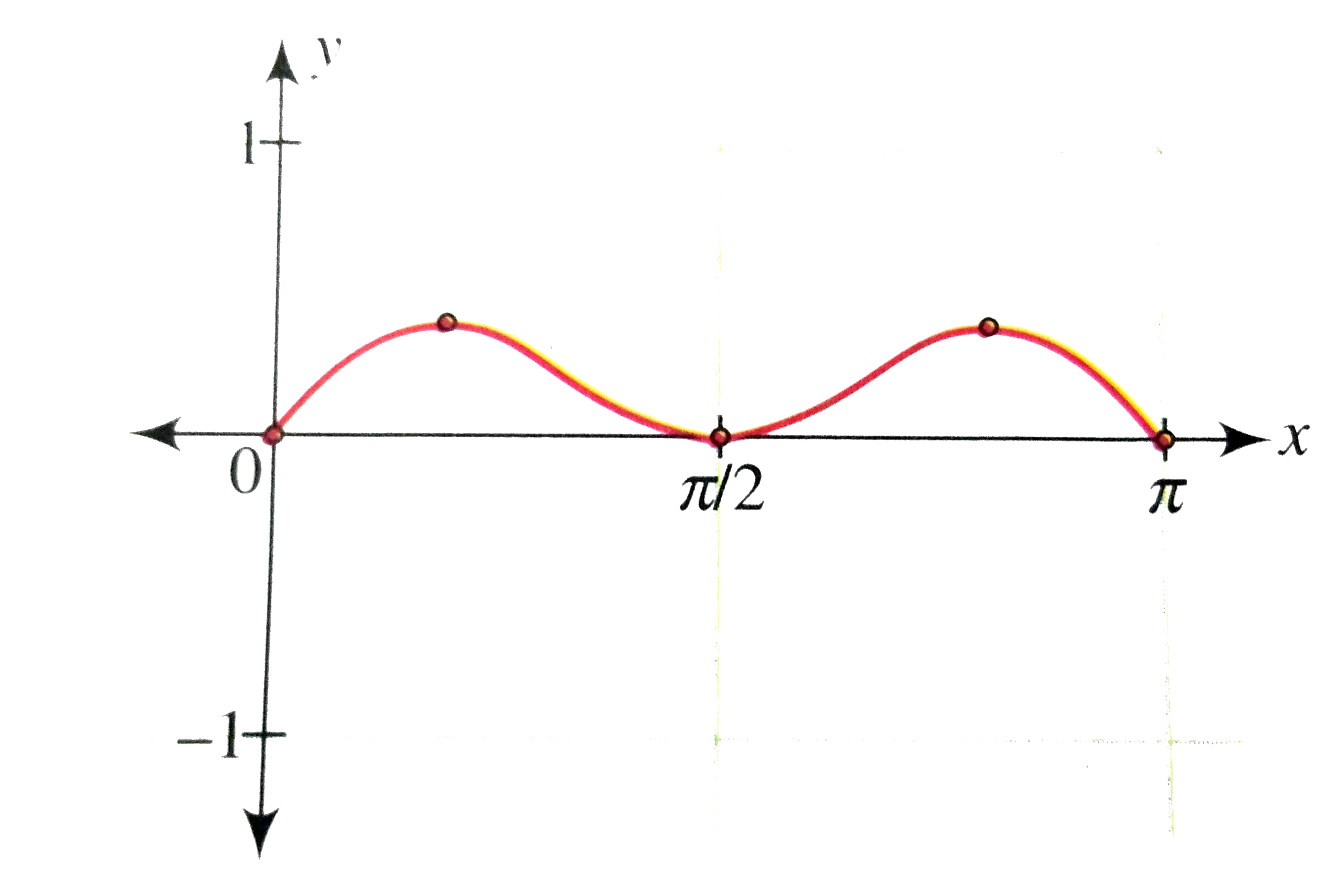
Hence the graph of y=f(x) for 0<x<π is as shown in the following figure.
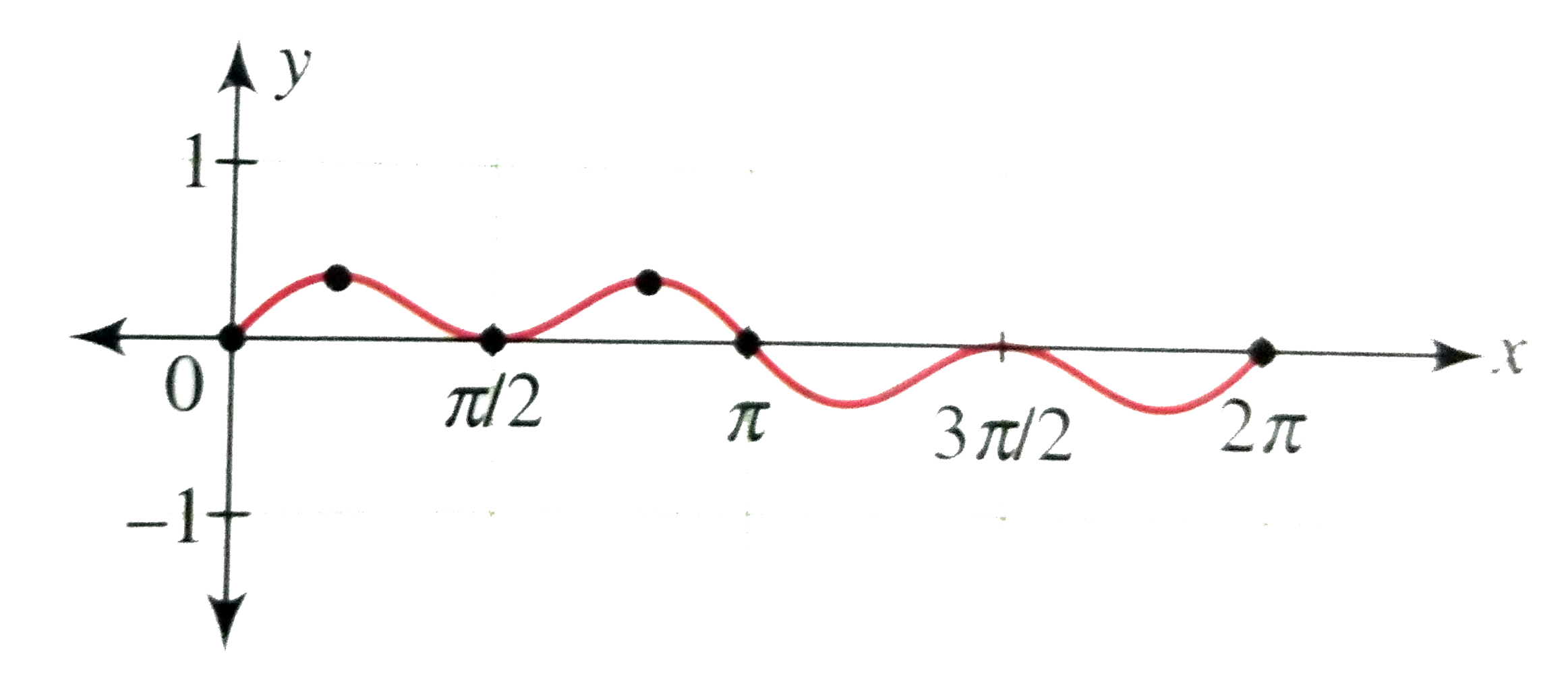
For π<x<2π, the graph of y=f(x) lies below the x-axis.
Hence, the graph of y=f(x) for π<x<2π is as shown in the following figure.
Since the period of f(x) is 2π, the graph for R is as follows:
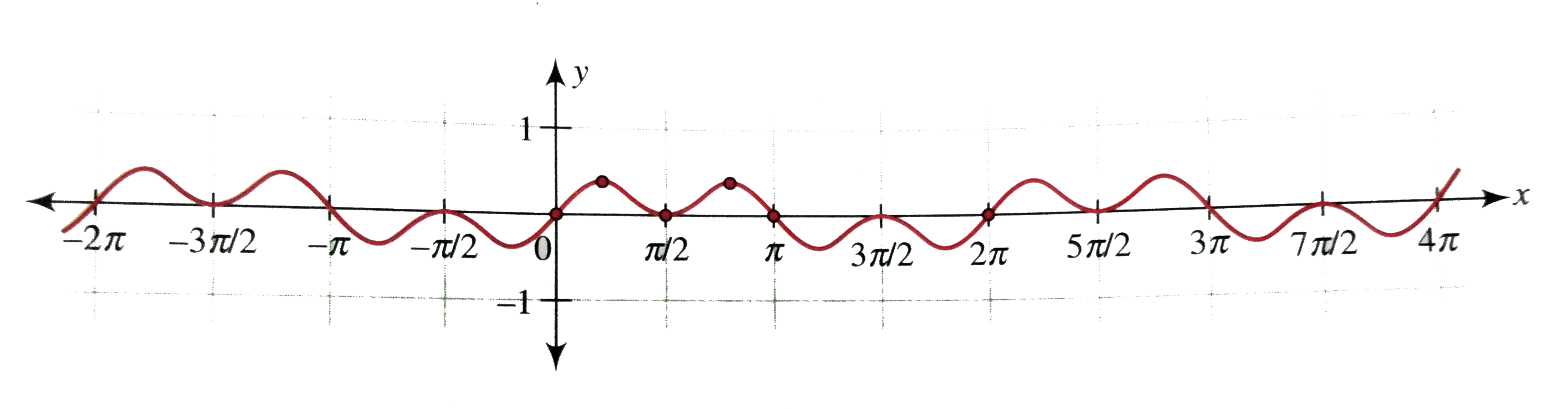
|
Topper's Solved these Questions
Similar Questions
Draw the graph of y=x−sinx
View SolutionDraw the graph of y=2x.
View SolutionDraw the graph of y=|x|
View SolutionDraw the graph of y=sin|x|.
View SolutionDraw the graph of y=sin2x−cosx
View SolutionDraw the graph of y=|x|+2
View SolutionDraw the graph of y=cos2x.
View SolutionDraw the graph of y≤x+2.
View SolutionDraw the graph of y=−x
View SolutionDraw the graph of y=3sin2x.
View Solution
