Draw the graph of y=xex. Find the range of the function. Also find the point of inflection.
We have y=f(x)=xex
Clearly, the domain of the function is R.
f(0)=−0
and f(x)=0 when x=0
f′(x)=ex+xex=ex(1+x)
f′(x)>0 for x<−1, where f(x) increases
f′(x)<0 for x<−1, where f(x) decreases
f′(x)=0∴x=−1
Also at x=−1,dydx, Changes sign from negative to positive, hence x=−1 is the point of minima,
f(−1)=−e−1=−1/e
When x→∞,f(x)→∞
Also limx→−∞xex=xx→−∞e−x=1x→−∞−e−x=0
So x-axis is an asymptote.
Thus, in (−∞,−1),f(x) decreases from 0+→−1/e
In (1,∞),f(x) increases, intersecting the x-axis at x=0
f''(x)=ex(2+x)
f''(x)=0∴x=−2
So x=−2 is the point of inflection.
From the above discussion, the graph of the function is as follows:
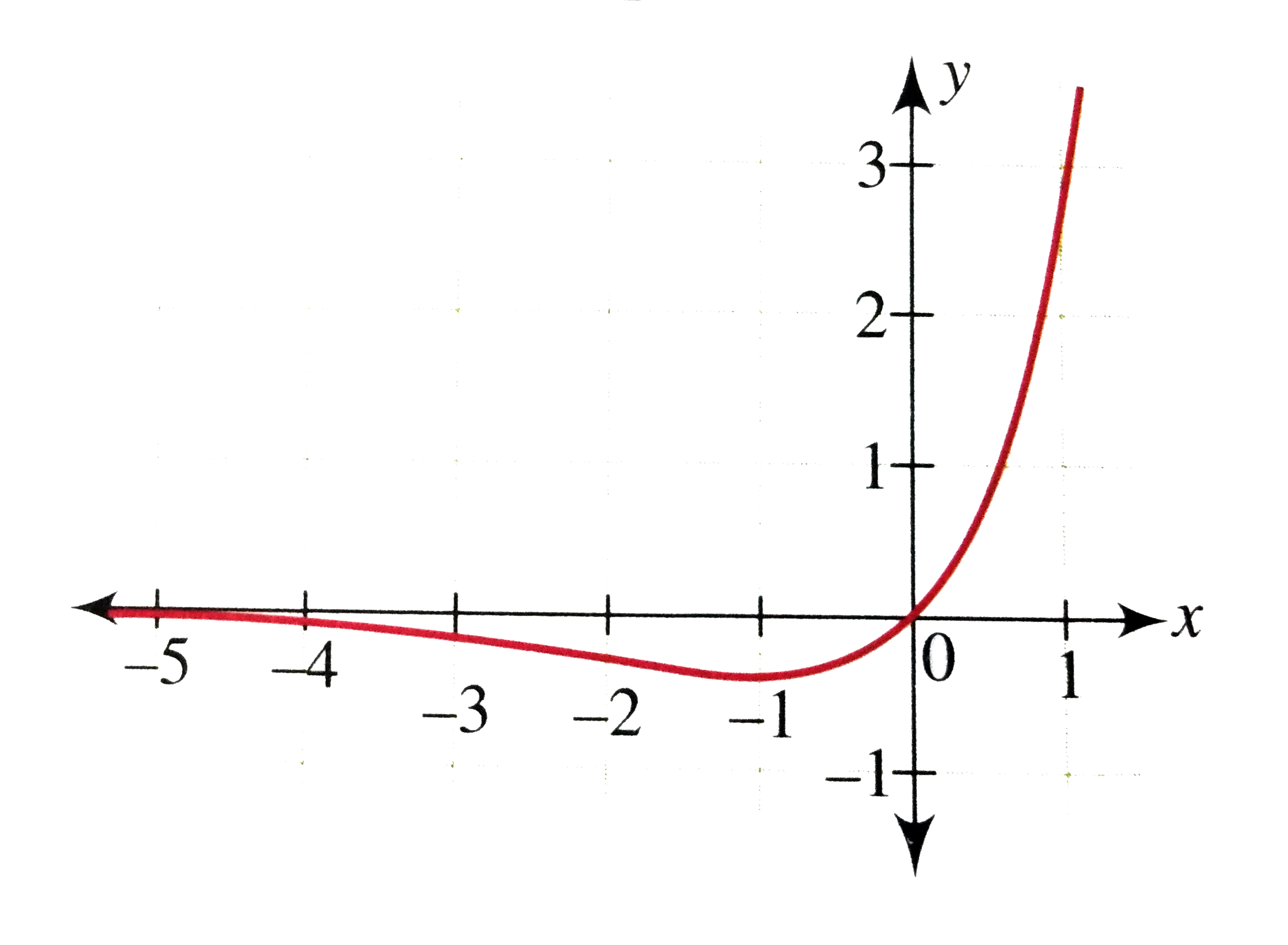
Range of the function is [f(−1),∞) or [−e−1,∞).
Topper's Solved these Questions
Similar Questions
Draw the graph of y=xex.Also
(i) Find the range of the functionf
(ii) Find the point of inflection.
(iii)Find the values of k if 1xex=k has two distinct real roots
View SolutionDraw the graph of f(x)=|x|−|2x−3|. Find the range of the function.
View SolutionDraw the graph of f(x)=|2x−1|+|2x−3|. Find the range of the function.
View SolutionDraw the graph of f(x)=|x−1|+|2x−3|. Find the range of the function.
View SolutionDraw the graph of f(x)=loge(√1−x2).Find the range of the function .Also find the values of k if (x) has two distinct real roots.
View SolutionFind the range of function y=ln(2x−x2)
View SolutionDraw the graph of y = tan x and find the period.
View SolutionDraw the graph of f(x)=2x+3x2/3 and discuss the type of non-differentiability for the function. Also find the point of inflection.
View SolutionLet f(x)=[x]+1{x}+1 for f:[0,52)→(12,3], where [⋅] represents the greatest integer function and {⋅} represents the fractional part of x.
Draw the graph of y=f(x). Prove that y=f(x) is bijective. Also find the range of the function.
View SolutionDraw the graph of f(x)sin−1|sinx|+cos−1(cosx). Find the range of the function. Find the points of non-differentiability. Also find the value of ∫10π0[sin−1|sinx|+cos−1(cosx)] dx
View Solution