Let f(x)=[x]+1{x}+1 for f:[0,52)→(12,3], where [⋅] represents the greatest integer function and {⋅} represents the fractional part of x.
Draw the graph of y=f(x). Prove that y=f(x) is bijective. Also find the range of the function.
Video Solution
Text Solution
We have f(x)=[x]+1{x}+1
=⎧⎪
⎪
⎪
⎪⎨⎪
⎪
⎪
⎪⎩1x+1,0≤x<12x,1≤x<23x−1,2≤x<52
Each branch of the function is part of a rectangular hyperbola.
The graph of the function is as shown in the function is as shown in the following figure.
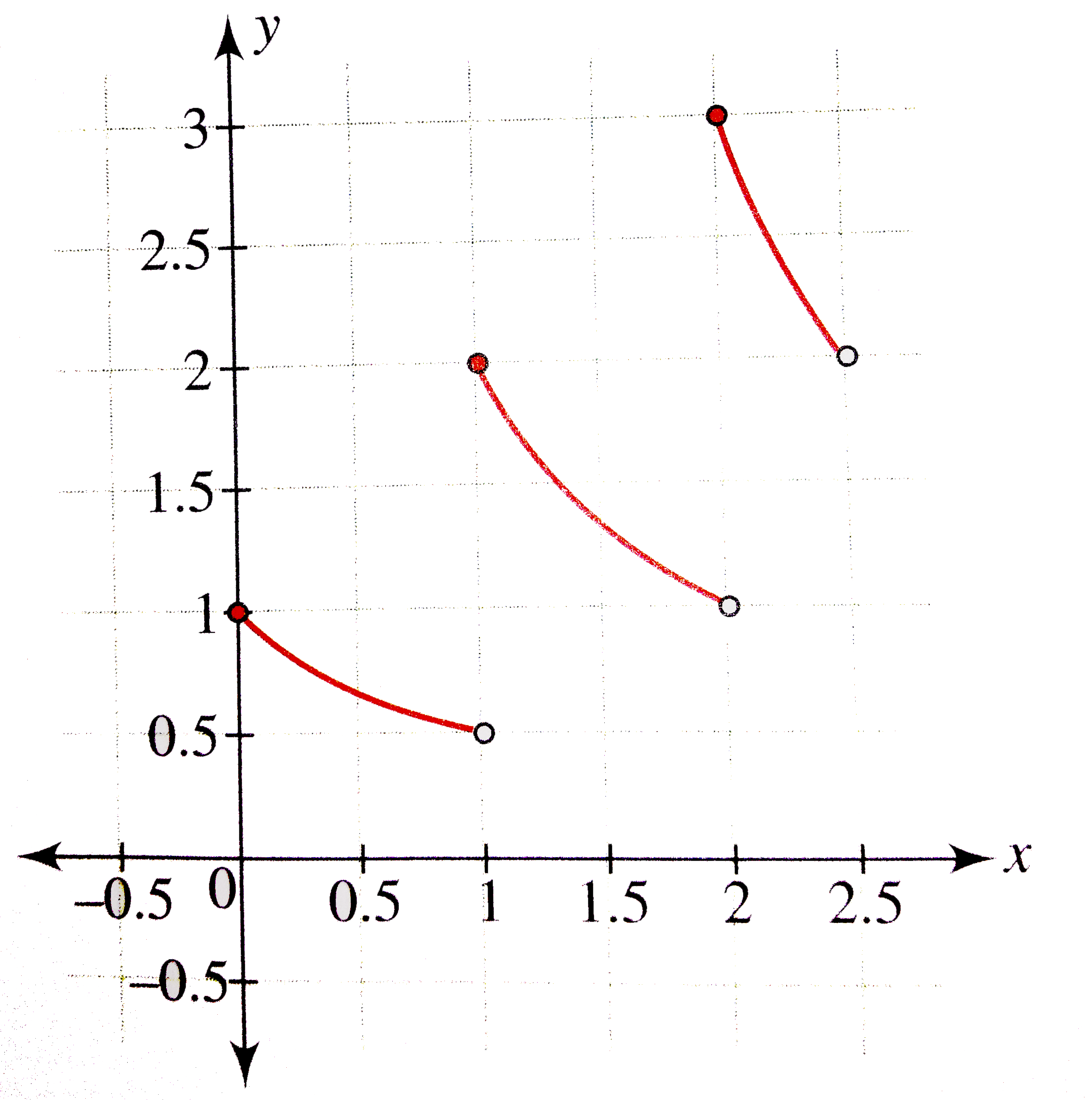
From the figure, the range of the function is [1/2,3].
Clearly, f(x) is a bijective function.
|
Topper's Solved these Questions
- GRAPHS OF ELEMENTARY FUNCTIONS Book:CENGAGEChapter:GRAPHS OF ELEMENTARY FUNCTIONS Exercise:Exercise
Explore 34 Videos
- GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSBook:CENGAGEChapter:GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSExercise:Exercise
Explore 13 Videos
- GRAPHS OF TRIGONOMETRIC FUNCTIONSBook:CENGAGEChapter:GRAPHS OF TRIGONOMETRIC FUNCTIONSExercise:Exercise
Explore 22 Videos
Similar Questions
Knowledge Check
f(x)=[x]+1{x}+1forf:[0,52)→(12,3], where [.] repesents the greatest integer function and {.} represents the fractional part of x then which of the following is true ?
Af(x) is injective discontinuous funtionBf(x) f(x) is surjective non - differntiable function .Cmin(limx→1−f(x),limx→1+f(x))=f(1).Dmax ( x values of point of discontinuity function .Let f(x) = [x] and [] represents the greatest integer function, then
Alimf(x)=1x→1+Blimx→2008−f(x)=2007Climx→kf(x)=2008,K∈(2008,2009)Dlimx→2008−x−[x]=1Let f(x)=[x]−[sinx]1−sin[cosx] and g(x)=1f(x) and [] represents the greatest integer function, then
Alimx→0f(x) existB1x→0g(x) existsClimx→0g(x) does not existsDlimx→0f(x)=0
f:(2,3)−−→0,1def∈edbyf(x)=x−[x],where[.] represents the greatest integer function.
View SolutionDraw a graph of f(x)=sin{x}, where {x} represents the greatest integer function.
View SolutionDraw the graph of f(x)=[tan−1x], where [⋅] represents the greatest integer function.
View SolutionFind the range of f(x)=x−[x]1−[x]+x',where[] represents the greatest integer function.
View SolutionDraw the graph of f(x)=cosπ[x], where [⋅] represents the greatest integer function. Find the period of the function.
View Solution

