The function f(x)=max.{(1−x),(1+x),2},x∈(−∞,∞) is
Continuous at all points
Differentiable at all points
Differentiable at all points except at x=1andx=−1
Continuous at all points except at x=1andx=−1, where it is discontinuous
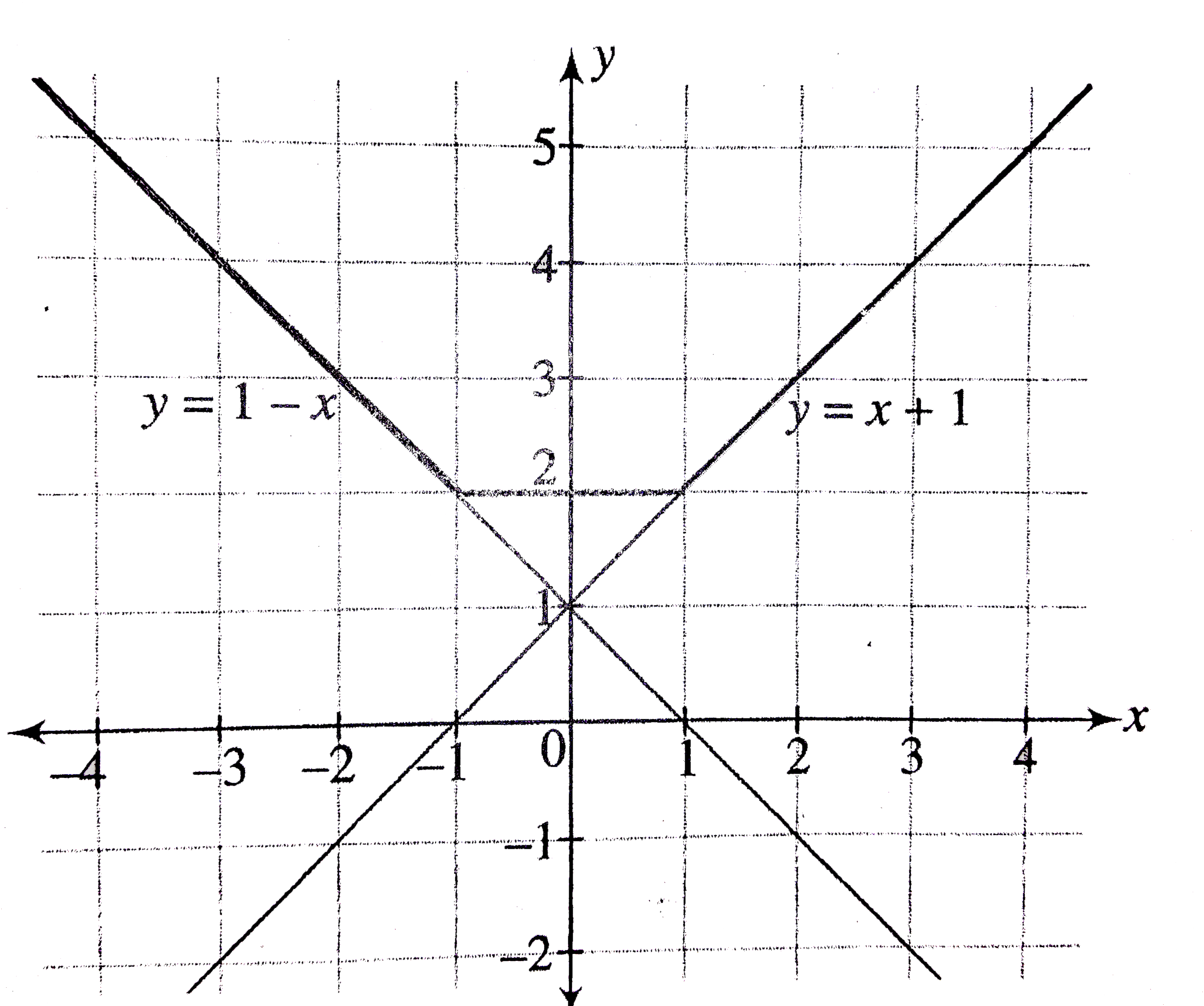
From the graph, y=f(x) is non-differentiable at x=±1.
Topper's Solved these Questions
- GRAPHS OF ELEMENTARY FUNCTIONS Book:CENGAGEChapter:GRAPHS OF ELEMENTARY FUNCTIONS Exercise:Exercise
Explore 34 Videos
- GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSBook:CENGAGEChapter:GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSExercise:Exercise
Explore 13 Videos
- GRAPHS OF TRIGONOMETRIC FUNCTIONSBook:CENGAGEChapter:GRAPHS OF TRIGONOMETRIC FUNCTIONSExercise:Exercise
Explore 22 Videos
Similar Questions
Knowledge Check
The greatest and the least value of the function, f(x)=√1−2x+x2−√1+2x+x2,x∈(−∞,∞) are
A2,-2B2,-1C2,0Dnone
The domain of the function f(x)=sin−1(|x|+5x2+1) is
(−∞,−a]∪[a,∞). then a is equal to :
View SolutionThe function f(x)=[14(3x2+1),−∞<x≤1;5−4x,1<x<4;4−x,4≤x<∞ is
View SolutionThe function f(x)=x1+|x| is differentiable on (A) (0 oo) 0 oo) (B) (-oo 0) (C) (D) all the above
View SolutionThe function f(x)=logx−2xx+2 is increasing for all
A) x∈(−∞,0),
B) x∈(−∞,1)
C) x∈(−1,∞)
D) x∈(0,∞)
View Solutionif f(x)=max{x2,x3,164} for all x∈(0,∞)
View SolutionThe number of points at which the function f(x)=max{a−x,a+x,b},−∞<x<∞,0<a<b cannot be differentiable is :
View SolutionThe domain of the function f(x)=1√|x|−x is:
(A) (−∞,∞)
(B) (0,∞
(C) (−∞,0)
(D) (−∞,∞)-{0}
View Solution

