Question

Draw the graph of $f\left(x\right)=|2x-1|+|2x-3|$. Find the range of the function.

Explanation

Function `f(x)= |2x-1|+ |2x-3|` changes definition where `2x-1=0 and 2x-3=0 or x=1//2 and x=3//2`.
Thus, we find the function in each of the intervals `(-oo, 1//2), (1//2, 3//2) and (3//2, oo)`.
`therefore " "f(x)= |2x-1|+ |2x-3|= {{:(1-2x+3-2x",",,x lt(1)/(2)),(2x-1+3-2x",",,(1)/(2)le xle (3)/(2)), (2x-1+2x-3",",,x gt(3)/(2)):}`
`" "= {{:(4-4x",",,xlt(1)/(2)),(2",",,(1)/(2)lexle(3)/(2)),(4x-4",",,xgt(3)/(2)):}`
Now we can draw the graph of each function in respective intervals.
Alternative method :
Since the graph of the function is linear in eah of the reagions `(-oo, 1//2), (1//2, 3//2) and (3//2, oo)`, we need to check the values of the function at some particular values of x to draw the graph in each region.
`" "f(1//2)=2`
`" "f(3//2)2`
`" "f(0)=4`
`" "f(2)=3+1=4`
Thus, we plot the points `A(0, 4), B(1//2, 2), C(3//2, 2) and D(2, 4)`. Plotting these points and connecting with the straight line, we have the following graph.

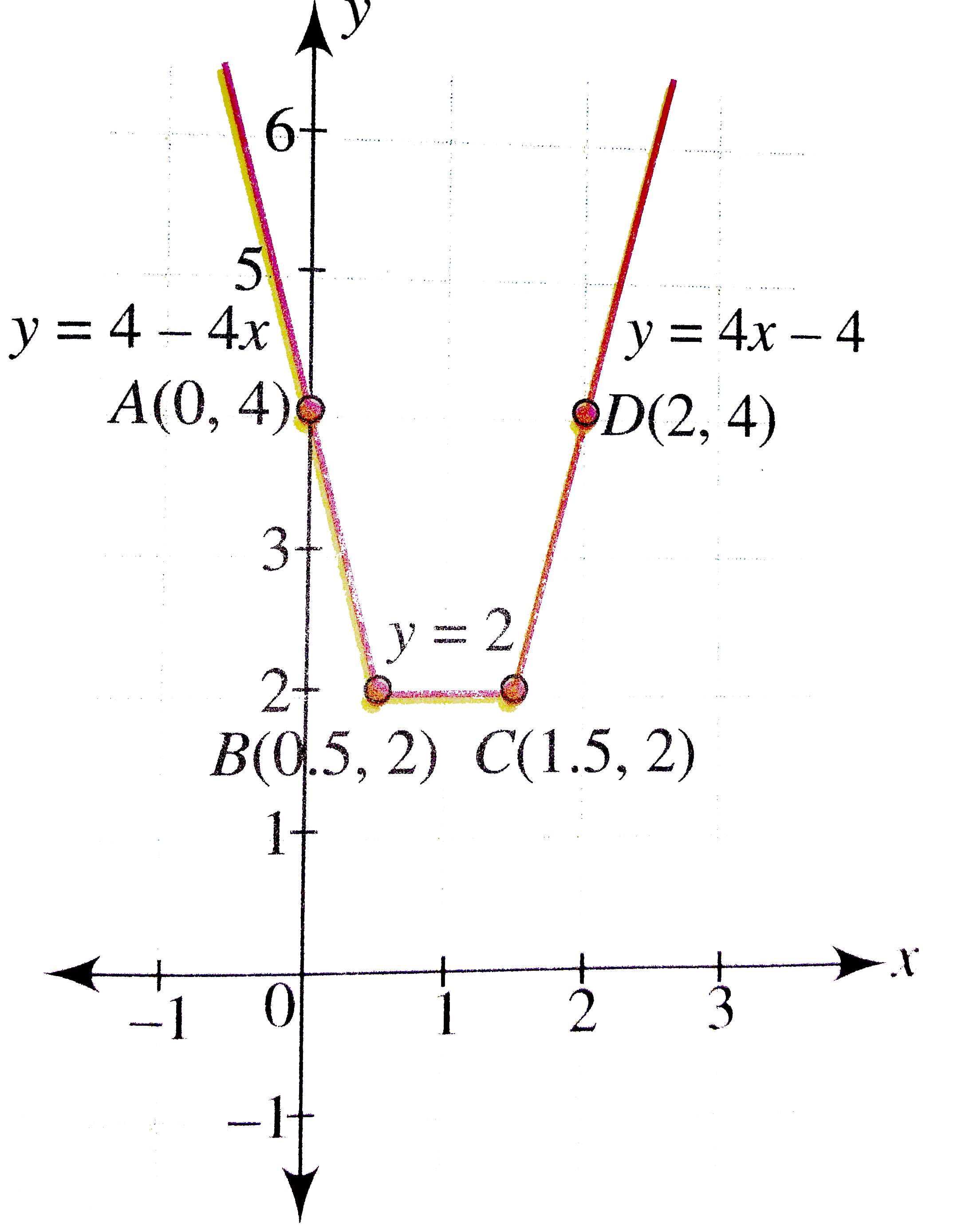
From the graph, the range of the function is `[2, oo)`.