For a point $P$ in the plane, let $d_{1} (P) a n d d_{2} (P)$ be the distances of the point $P$ from the lines $x - y = 0 a n d x + y = 0$ respectively. The area of the region $R$ consisting of all points $P$ lying in the first quadrant of the plane and satisfying $2 \leq d_{1} (P) + d_{2} (P) \leq 4,$ is

Video Solution

Text Solution

Verified by Experts

For $P (x, y)$ , we have
$2 \leq d_{1} (P) + d_{2} (P) \leq 4$
$\Rightarrow 2 \leq \frac{| x - y |}{\sqrt{2}} + \frac{| x + y |}{\sqrt{2}} \leq 4$ ltBrgt $\Rightarrow 2 \sqrt{2} \leq | x - y | + | x + y | \leq 4 \sqrt{2}$
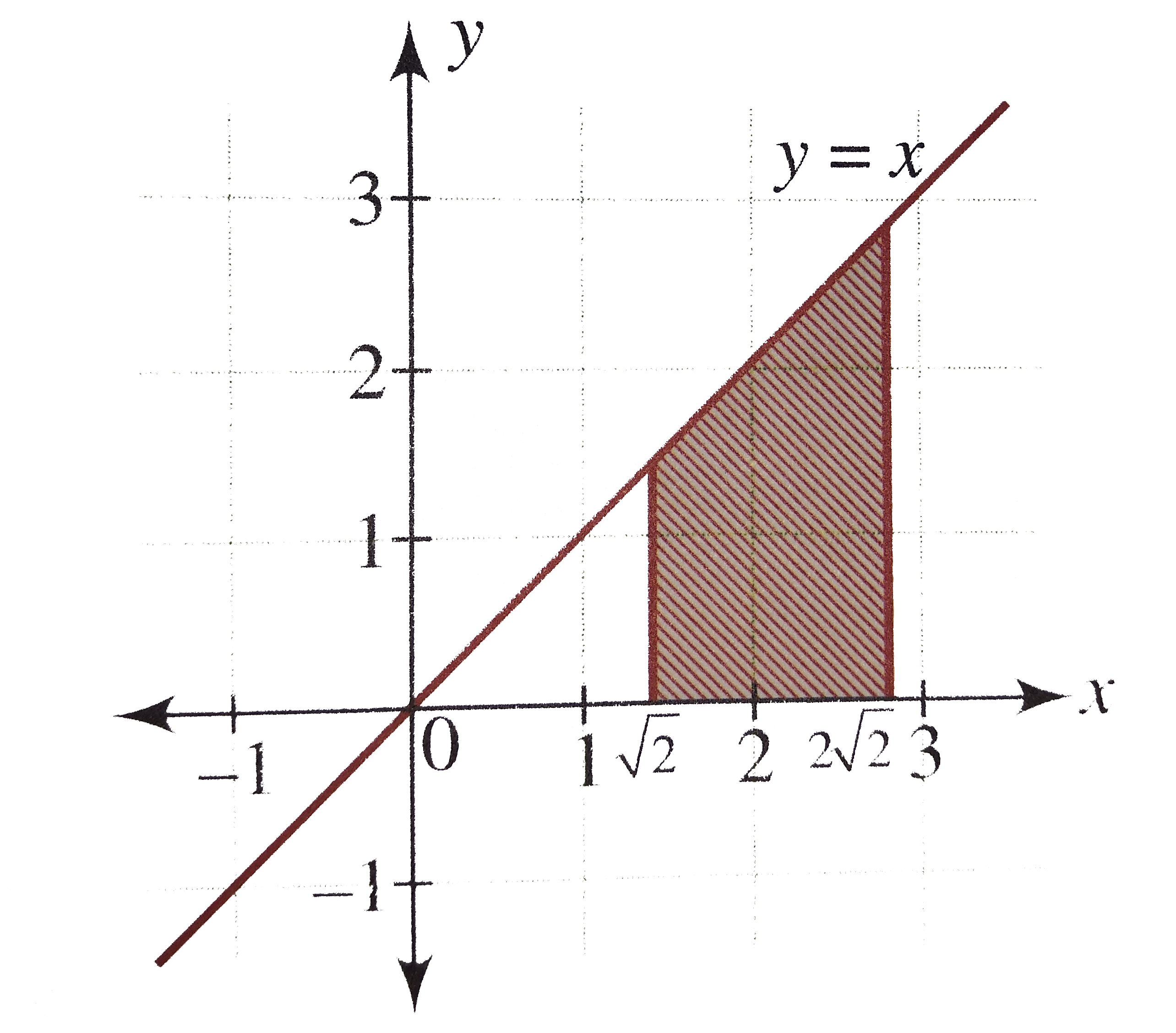
In the first quadrant if $x > y$ , we have
$2 \sqrt{2} \leq x - y + x + y \leq 4 \sqrt{2}$
or $\sqrt{2} \leq x \leq 2 \sqrt{2}$
The region of points satisfying these inequalities is as follows.

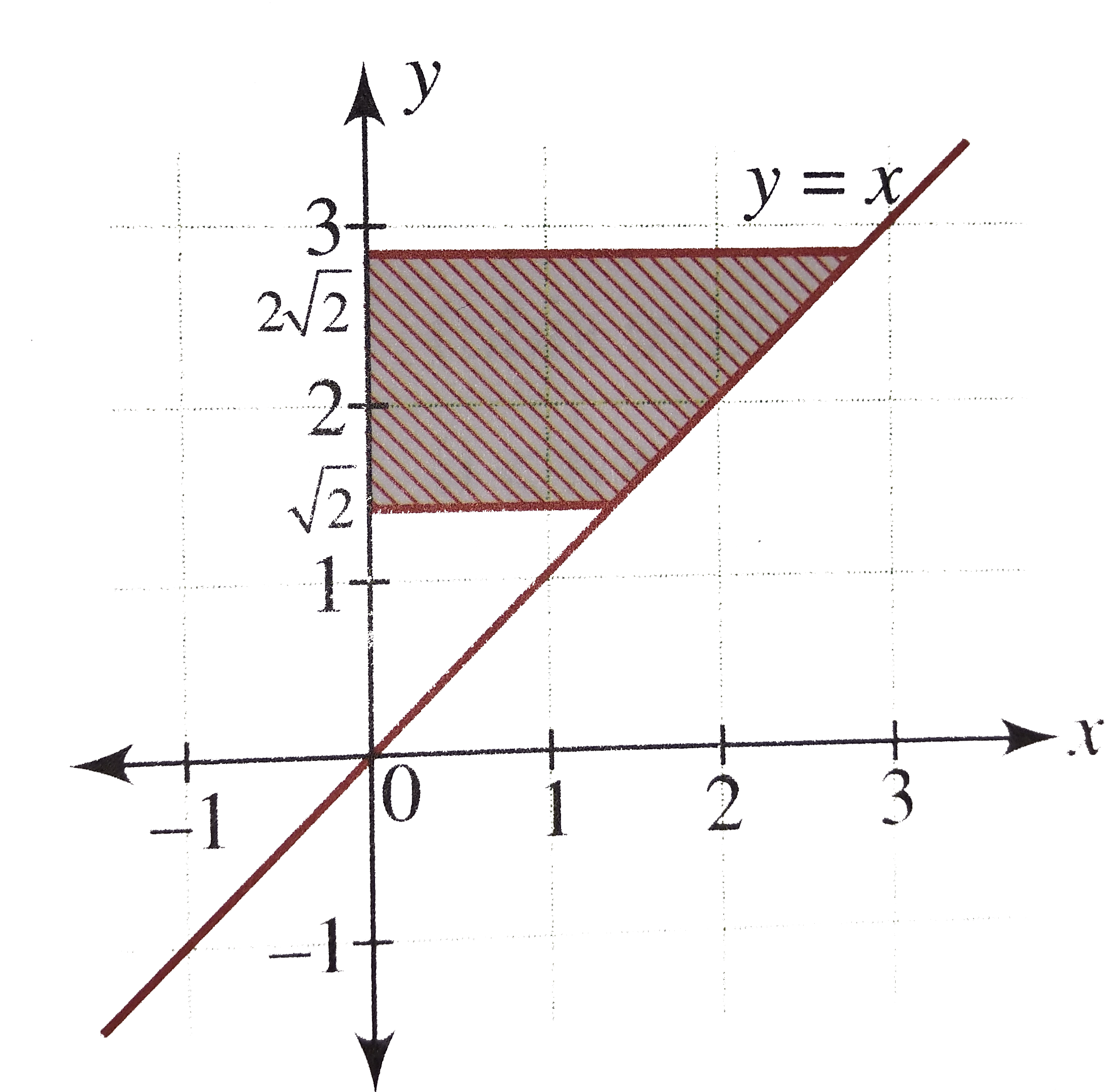
In the first quadrant if $x < y$ , we have
$2 \sqrt{2} \leq y - x + y \leq 4 \sqrt{2}$
or $\sqrt{2} \leq y \leq 2 \sqrt{2}$
The region of points satisfying these inequalities is as follows.

Combining the above two regions, we have the following.

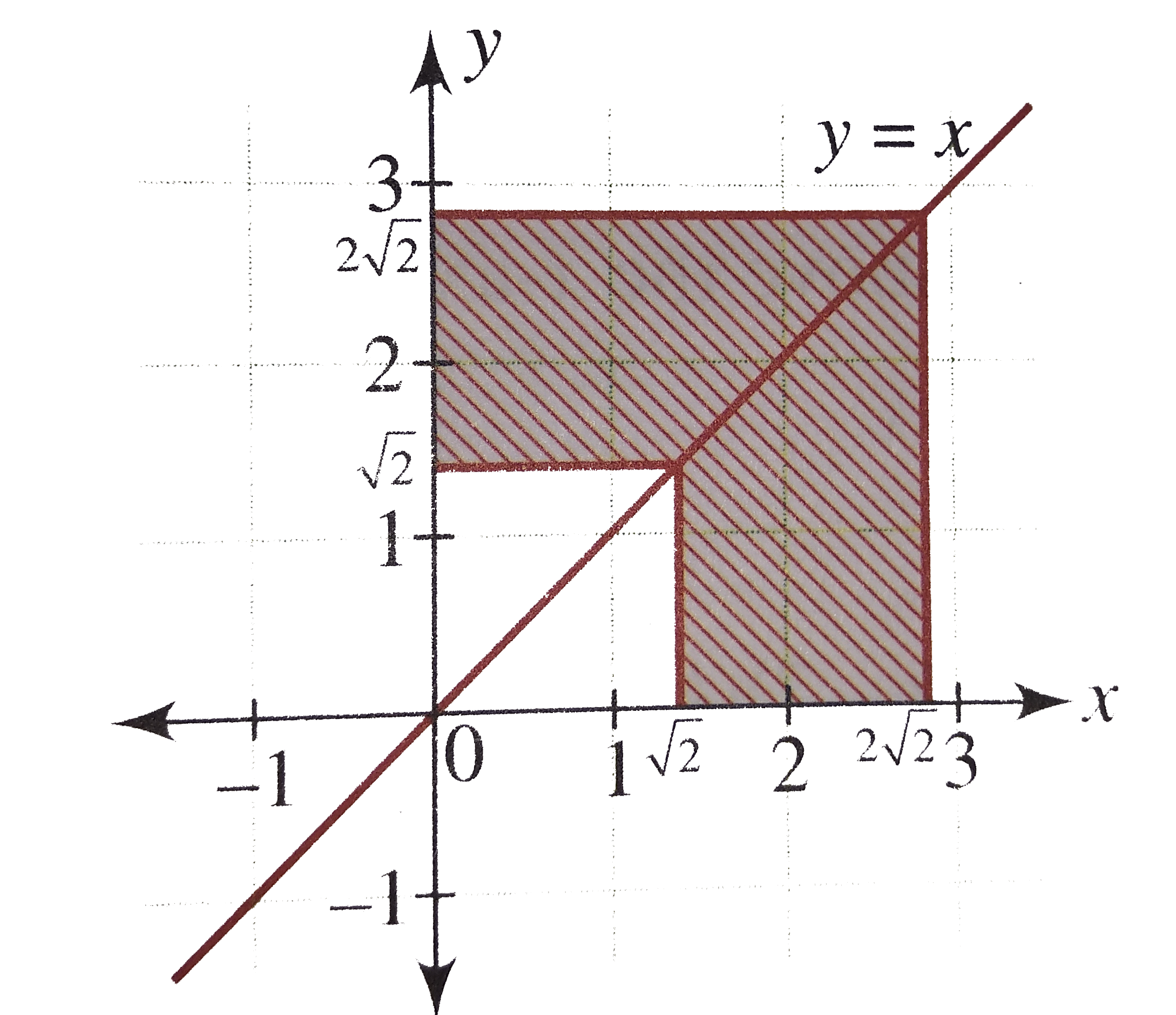
Area of the shaded region $= ({(2 \sqrt{2})}^{2} - {(\sqrt{2})}^{2})$
$= 8 - 2 = 6$ sq.units

Updated on:21/07/2023

|

Class 12 MATHS FUNDAMENTAL OF MATHEMATICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Let P be the set of points $(x, y)$ such that $x^{2} \leq y \leq - 2 x + 3$ . Then area of region bounded by points in set P is
A $\frac{16}{3}$
B $\frac{32}{3}$
C $\frac{29}{3}$
D $\frac{20}{3}$

CENGAGE-GRAPHS OF ELEMENTARY FUNCTIONS -Exercise

Home
Ask Doubt
Profile