The area of the region is 1st quadrant bounded by the y-axis, y=x4,y=1+√x,andy=2√x is
2/3 sq. units
8/3 sq. units
11/3 sq. units
13/6 sq. units
The correct Answer is:C
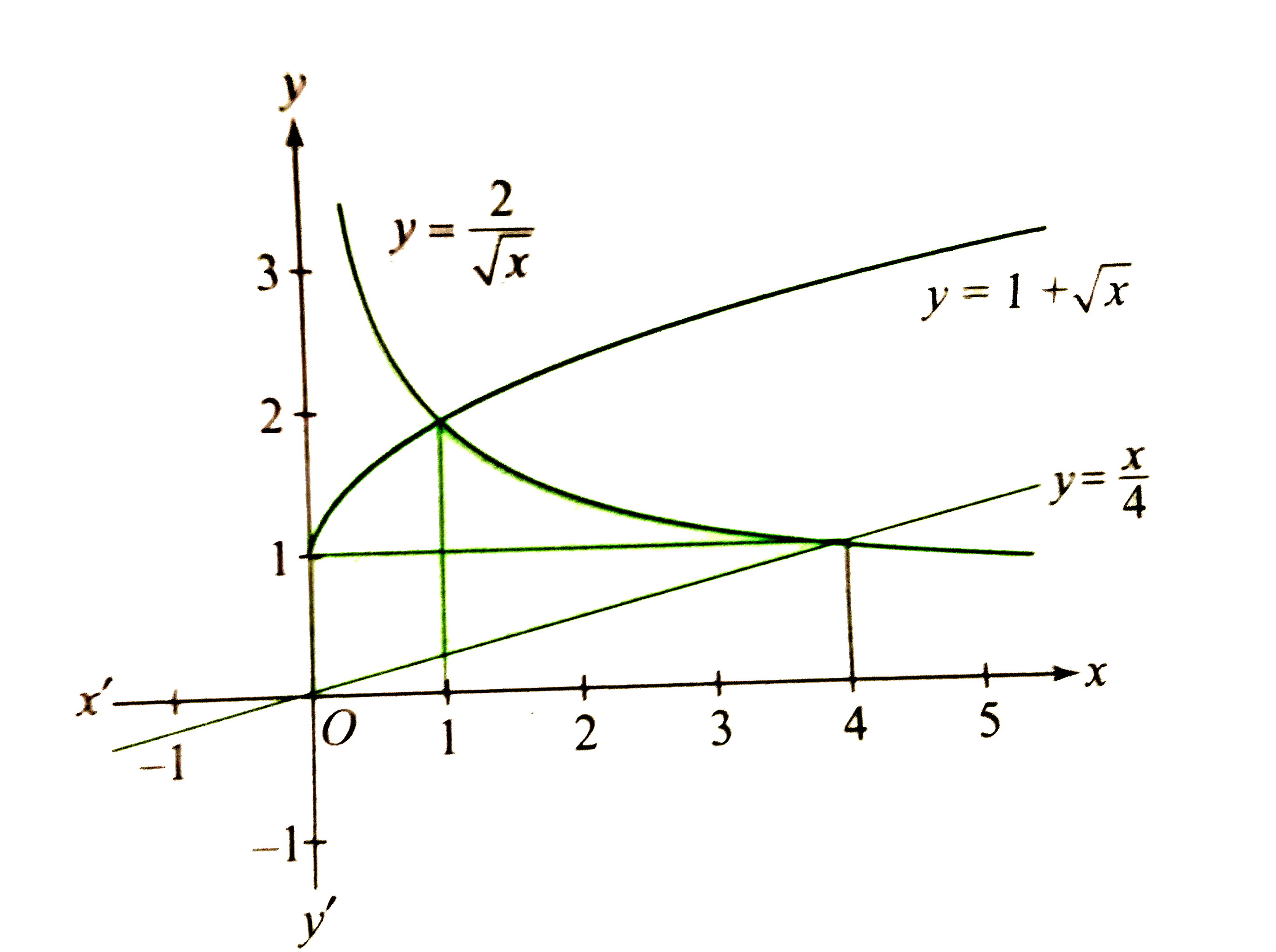
A1=1∫0(1+√x−x4)dx
=[x+2x3/23−x28]10=1+23−18=3724.
A2=4∫1(2√2−x4)dx
=[4√x−x28]41
[8−2−4+18]=178
or A=A1+A2=8824=113 sq. units.
Topper's Solved these Questions
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise (Multiple)
10 Videos
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise (Comprehension)
21 Videos
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise 9.3
7 Videos
- APPLICATIONS OF DERIVATIVESBOOK - CENGAGECHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Question Bank
29 Videos
- AREA UNDER CURVESBOOK - CENGAGECHAPTER - AREA UNDER CURVESEXERCISE - Question Bank
20 Videos
Similar Questions
The area of the region in Ist quadrant bounded by y-axis, y=x4,y=1+√x and y=2√x is equals to ……..
View SolutionLet A be the area of the region in the first quadrant bounded by the x-axis the line 2y = x and the ellipse x29+y21=1. Let A' be the area of the region in the first quadrant bounded by the y-axis the line y = kx and the ellipse . The value of 9k such that A and A' are equal is _____
View Solution
Knowledge Check
The area of the region bounded by y = x - 1 and x=3−y2 is
A52B72C92D4The area of the region bounded by the lines y=2x+1y=3x+1 and x=4 is
A16 sq unitB1213 sq unitC1216 sq unitD8 sq unitThe area of the region bounded by y=|x−1|andy=3−|x|, is
A2B3C4D1
Find the area of the region lying in the first quadrant and bounded by y=4x2,x=0,y=1andy=4.
View SolutionFind the area of region in the first quadrant, bounded by line 2y=x, ellipse x24+y2=1
View SolutionConside the line x=√3y and the circle x2+y2=4
What is the area of the region in the first quadrant enclosed by the X-axis, the line =√3y and the circle?
View SolutionThe area of the region bounded by x=y2−y and Y-axis is
View SolutionThe area of the region bounded by the curve y=sin2x, y-axis and y=1 is :
View Solution
